Решение произвольных систем уравнений. Метод Гаусса.
Пусть задана система m линейных уравнений с n неизвестными:
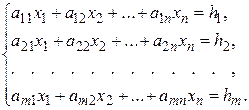 (1)
(1)
Рассмотрим один из самых простых методов решения систем уравнений, заключающийся в последовательном исключении неизвестных и называемый методом Гаусса. Данный метод заключается в том, что с помощью элементарных преобразований строк расширенной матрицы системы уравнений, она приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних по номеру переменных, находятся все остальные. Метод Гаусса имеет ряд преимуществ:
1) значительно менее трудоёмкий;
2) позволяет однозначно установить, совместна система или нет, а в случае её совместности найти её решения (единственное или бесконечное множество);
3) дает возможность определить ранг матрицы системы.
С помощью элементарных преобразований над строками приведем расширенную матрицу системы (2.1) (А|В) к ступенчатому виду (А`|Н`):
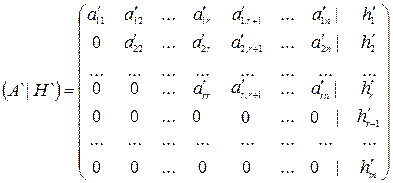 ,
,
где 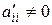 при
при 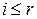 .
.
Полученной расширенной матрице (А`|Н`) соответствует система линейных уравнений, эквивалентная системе (2.1). При этом r(A) = r(A`), r(A`|Н`) = r(A|Н), и утверждения о том, что полученная система совместна (несовместна) и определена (неопределенна) верны и для системы (2.1).
Если хотя бы одно из чисел 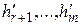 отлично от нуля, то система линейных уравнений несовместна.
отлично от нуля, то система линейных уравнений несовместна.
Если же 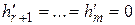 , то система совместна, ее ранг равен r. Очевидно, что минор, стоящий на пересечении первых r строк и r столбцов, не равен нулю, следовательно, его можно принять за базисный. Назовем переменные
, то система совместна, ее ранг равен r. Очевидно, что минор, стоящий на пересечении первых r строк и r столбцов, не равен нулю, следовательно, его можно принять за базисный. Назовем переменные 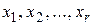 базисными, а
базисными, а 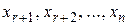 - свободными. Отбрасывая строки с нулевыми элементами, получаем систему из r уравнений:
- свободными. Отбрасывая строки с нулевыми элементами, получаем систему из r уравнений:
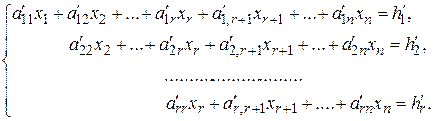 (1)
(1)
Если r = n , то матрица этой системы треугольная, все переменные – базисные, и их значения определяются однозначно.
Если r < n, то из системы легко выразить базисные переменные через свободные переменные. Придавая свободным переменным произвольные значения:
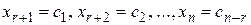 ,
,
последовательно получаем выражения для базисных переменных
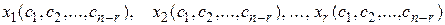 .
.
Определение . Решение, задаваемое формулами
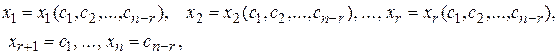
где 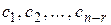 - любые действительные числа, называется общим решением системы (2.1).
- любые действительные числа, называется общим решением системы (2.1).
Пример 1. Решить методом Гаусса систему уравнений
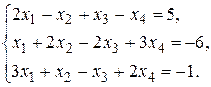
Составим расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду
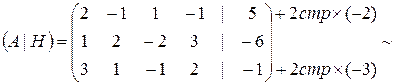
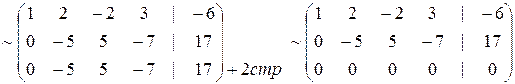 .
.
r(A) = r(A|Н) = 2 < 4, следовательно, система имеет бесконечное множество решений.
Исходная система равносильна системе:
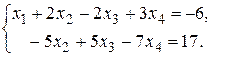
Решим ее.
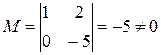 , этот минор можно принять за базисный. Тогда, x1, x2 – базисные переменные, а остальные x3, x4 – свободные переменные.
, этот минор можно принять за базисный. Тогда, x1, x2 – базисные переменные, а остальные x3, x4 – свободные переменные.
Задавая свободным переменным произвольные значения x3 = c1, x4 = c2 найдем бесконечное множество решений.
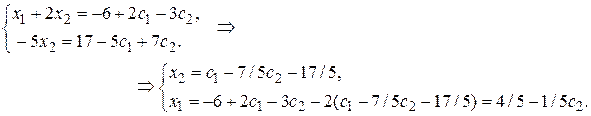
Ответ: 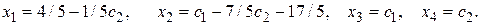
Дата добавления: 2015-08-21; просмотров: 870;
