Атом водорода.
В нерелятивистском приближении стационарные состояния атома определяются уравнением Шредингера для системы электронов, движущихся в кулоновском поле ядра и электрически взаимодействующих друг с другом.
В то же время единственным атомом, для которого уравнение Шредингера может быть решено точно, является простейший из всех атомов – атом водорода.
Задача о движении двух взаимодействующих частиц в квантовой механике аналогично тому, как это делалось в классической механике, сводится к решению задачи о движении одной частицы в поле центральных сил.
В центральном (или центрально-симметричном) поле потенциальная энергия взаимодействия 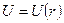 зависит только от модуля разности координат взаимодействующих частиц.
зависит только от модуля разности координат взаимодействующих частиц.
Уравнение Шредингера движения частицы в центрально-симметричном поле имеет вид:
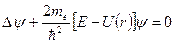 .
.
В атоме водорода электрон обладает потенциальной энергией
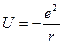 ,
,
где 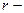 координата электрона, отсчитываемая от центра поля, т.е. от ядра.
координата электрона, отсчитываемая от центра поля, т.е. от ядра.
Можно несколько расширить класс рассматриваемых решений, если ввести в рассмотрение так называемый водородоподобный атом с зарядом ядра 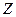 . Тогда уравнение Шредингера запишется в виде:
. Тогда уравнение Шредингера запишется в виде:
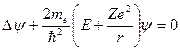 . (*)
. (*)
Поскольку задача обладает сферической симметрией, то для её решения воспользуемся выражением для оператора Лапласа в сферических координатах:
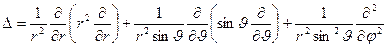 .
.
Т.о., мы приходим к уравнению (*) относительно трех переменных: 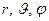 .
.
Попытаемся разделить переменные, представив волновую функцию 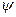 (ищем решение уравнения (*))в виде:
(ищем решение уравнения (*))в виде:
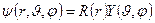 , (**)
, (**)
где 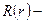 ”радиальная” функция;
”радиальная” функция;  сферические функции.
сферические функции.
Произведя дифференцирование, получим
 ,
,
поделив на 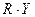 и домножив на
и домножив на 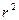 , имеем
, имеем
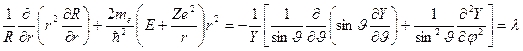 .
.
Очевидно, что функции, стоящие по обе стороны в первом равенстве, зависят от совершенно разных переменных, поэтому 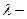 просто число. Т.о., приходим к двум независимым уравнениям.
просто число. Т.о., приходим к двум независимым уравнениям.
Первое
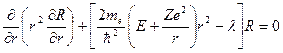 ,
,
и второе
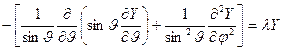 . (****)
. (****)
Заметим, что выражение
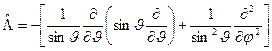
называется оператором Лежандра. Поэтому уравнение (****) можно записать как
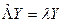 .
.
Обратимся сначала к уравнению (****). Произведем теперь разделение угловых переменных, представив функцию 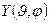 как
как
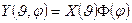 .
.
После подстановки в (****) получаем
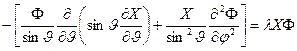 .
.
Поделив последнее уравнение на произведение  и домножив на
и домножив на 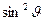 , получаем
, получаем
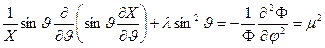 . (*****)
. (*****)
Как и в предыдущем случае, очевидно, что 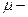 число.
число.
Начнем опять со второго равенства.
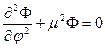 . (+)
. (+)
Общее решение этого уравнения можно представить в виде линейной комбинации экспонент с комплексными фазами:
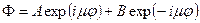 . (++)
. (++)
Постоянная 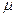 может быть определена, если учесть очевидное требование, которому должна удовлетворять функция
может быть определена, если учесть очевидное требование, которому должна удовлетворять функция 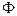 :
:
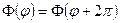 . (+++)
. (+++)
Подставляя (++) в (+++), получаем
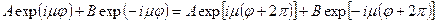 ,
,
что, очевидно, может быть лишь когда
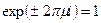 ,
,
или
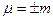 , (++++)
, (++++)
где 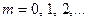
Т.о.,
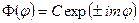 .
.
Обратимся теперь к первому из уравнений (*****), преобразовав его с учетом (++++) к виду
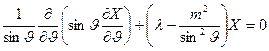 .
.
Это, так называемое уравнение Лежандра, которое имеет непрерывное (т.е. нужное нам) решение только при
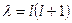 , причем
, причем 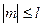 . (5+)
. (5+)
Решением уравнения Лежандра являются присоединенные полиномы Лежандра, обозначаемые как 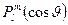 .
.
Например,
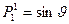 ;
; 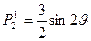 ;
; 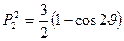 и т.д.
и т.д.
Обратимся, наконец, к радиальной части уравнения Шредингера, приняв во внимание (5+):
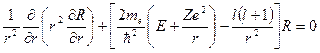 . (6+)
. (6+)
Это уравнение может быть приведено к виду:
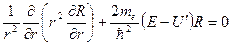 ,
,
где 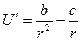 (см. рис.).
(см. рис.).
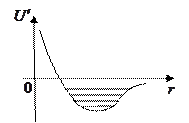
Можно показать, что частица, движущаяся в поле, характеризуемом потенциалом  , имеет непрерывный
, имеет непрерывный
Спектр энергий при 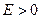 и дискретный, когда
и дискретный, когда 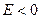 .
.
Введем новую переменную – безразмерную координату электрона
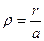 .
.
Теперь уравнение (6+) принимает вид:
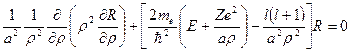 ,
,
или, умножив на 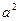
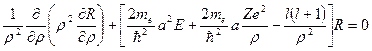 (7+)
(7+)
и положив параметр 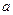 равным
равным
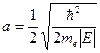 ,
,
и обозначив
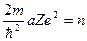 ,
,
приводим уравнение (6+) к виду:
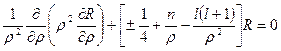 . (8+)
. (8+)
В математической физике показывается, что уравнение (8+) имеет конечное однозначное и непрерывное решение, причем
1. если первое слагаемое в квадратных скобках равно 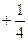 , то решение существует при произвольном положительном
, то решение существует при произвольном положительном 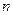 (
( 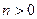 ). Поскольку
). Поскольку  , то энергия положительная и меняется непрерывно;
, то энергия положительная и меняется непрерывно;
2. при значении 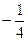 решение существует только для целых
решение существует только для целых 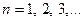 , где
, где 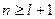 . Тогда спектр значений параметра
. Тогда спектр значений параметра 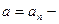 дискретный:
дискретный:
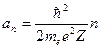 , соответственно
, соответственно 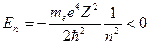 ,
,
что полностью совпадает с результатом, полученным в теории Бора.
Очевидно, что для каждого 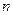 будем иметь собственную функцию
будем иметь собственную функцию 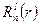 .
.
Понятно, что волновая функция электрона определяется произведением трех функций:
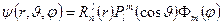 .
.
Целочисленные величины, определяющие волновую функцию электрона – квантовые числа – удовлетворяют следующим условиям:
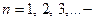 главное квантовое число, определяющее энергию электрона в атоме (для водородоподобного
главное квантовое число, определяющее энергию электрона в атоме (для водородоподобного
атома);
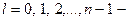 азимутальное квантовое число;
азимутальное квантовое число;
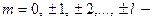 магнитное квантовое число.
магнитное квантовое число.
Необходимо особо подчеркнуть, что квантовомеханическое описание атома позволяет совершенно иначе подойти к интерпретации понятия “орбита электрона”, введенного в теории Бора-Зоммерфельда, нежели это следует из полуклассических представлений.
Рассмотрим основное состояние атома водорода, которое определяется набором квантовых чисел:
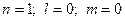 .
.
Уравнение Шредингера для радиальной функции электрона в основном состоянии принимает вид:
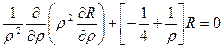 .
.
Его решение есть функция вида
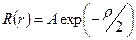 ,
,
в чем можно убедиться непосредственной подстановкой.
По смыслу функции 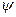 вероятность
вероятность 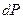 обнаружить электрон в элементарном объеме
обнаружить электрон в элементарном объеме 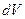 есть
есть
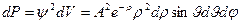 ,
,
где 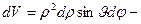 элементарный объем, записанный в сферических координатах.
элементарный объем, записанный в сферических координатах.
Вероятность найти электрон на расстоянии 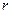 до
до 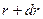 от ядра:
от ядра:
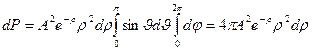 .
.
Наиболее вероятное расстояние электрона от ядра можно найти, взяв производную по 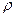 в последнем уравнении и положив её равной нулю:
в последнем уравнении и положив её равной нулю:
 ,
,
т.е. 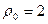 , или
, или
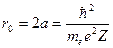 .
.
Это первый боровский радиус.
Дата добавления: 2015-08-08; просмотров: 2098;
