Самосопряженные (эрмитовы) операторы.
Самосопряженные операторы.
Если динамическая переменная, которой сопоставлен оператор 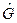 , представляет собой физическую величину, непосредственно измеряемую (“наблюдаемую”), то она является вещественной функцией, поэтому все результаты измерения величины
, представляет собой физическую величину, непосредственно измеряемую (“наблюдаемую”), то она является вещественной функцией, поэтому все результаты измерения величины 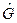 , а, следовательно, и средние значения также являются вещественными, каково бы ни было динамическое состояние системы, т.е. какой бы ни была волновая функция
, а, следовательно, и средние значения также являются вещественными, каково бы ни было динамическое состояние системы, т.е. какой бы ни была волновая функция 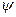 .
.
Действительно, при измерении физической величины 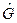 , могут быть реализованы следующие ситуации:
, могут быть реализованы следующие ситуации:
1) пусть физическая система (частица) в данный момент времени находится в состоянии, описываемом собственной функцией 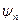 , тогда точное измерение величины
, тогда точное измерение величины 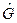 с достоверностью приведет к значению
с достоверностью приведет к значению 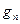
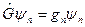 ;
;
2) пусть физическая система (частица) находится в некотором произвольном состоянии с волновой функцией 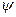 , которая в соответствии с принципом суперпозиции должна представлять собой линейную комбинацию тех из собственных функций
, которая в соответствии с принципом суперпозиции должна представлять собой линейную комбинацию тех из собственных функций 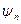 , которые соответствуют могущим быть обнаруженными с отличной от нуля вероятностью значениям
, которые соответствуют могущим быть обнаруженными с отличной от нуля вероятностью значениям 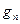 при измерении, произведенном над системой.
при измерении, произведенном над системой.
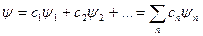 .
.
Тогда произведенное измерение величины 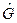 даст в результате одно из собственных значений
даст в результате одно из собственных значений 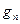 , которое, разумеется, тоже вещественно.
, которое, разумеется, тоже вещественно.
3)
…………
Это обстоятельство накладывает определенное ограничение на возможный вид (свойства соответствующих) операторов, а именно: ( 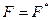
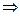
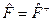 ).
).
Иначе говоря, оператор 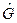 должен быть эрмитовым, или самосопряженным.
должен быть эрмитовым, или самосопряженным.
Операторы, соответствующие наблюдаемым (измеряемым) физическим величинам определяются равенством:
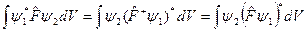 , (3.2.1)
, (3.2.1)
где 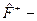 оператор, сопряженный оператору
оператор, сопряженный оператору 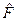 . Самосопряженные операторы
. Самосопряженные операторы
То есть, если
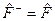 , (3.2.2)
, (3.2.2)
то этот оператор называется самосопряженным или эрмитовым оператором.
Анализируя равенство (3.2.1), можно сказать, что действие оператора 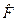 на стоящую справа от него функцию
на стоящую справа от него функцию 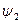 , совпадает с действием комплексно сопряженного ему оператора
, совпадает с действием комплексно сопряженного ему оператора 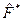 на стоящую слева от оператора
на стоящую слева от оператора 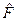 функцию
функцию 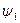 :
:
 (3.2.3)
(3.2.3)
---------------------------------
Примечание: понятие транспонированного оператора 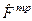 определяется из соотношения
определяется из соотношения
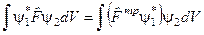 , (3.2.4)
, (3.2.4)
т.е. оператор, который дает тот же результат, действуя на левую функцию, как и 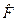 , действуя на правую. Таким образом, сопряженный оператор – это комплексно сопряженный оператор от транспонированного оператора:
, действуя на правую. Таким образом, сопряженный оператор – это комплексно сопряженный оператор от транспонированного оператора:
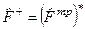 (3.2.5)
(3.2.5)
------------------------------------
Примеры.
1) Оператор координаты 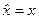 - эрмитов оператор.
- эрмитов оператор.
2) Рассмотрим оператор дифференцирования 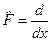 (будем считать, что волновые функции равны 0 на бесконечности
(будем считать, что волновые функции равны 0 на бесконечности 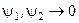 при
при 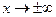 ). Вычислим сопряженный оператор:
). Вычислим сопряженный оператор:
………………..
Таким образом 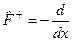 и оператор
и оператор 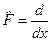 не является эрмитовым.
не является эрмитовым.
3) Оператор импульса 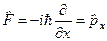 - самосопряженный:
- самосопряженный:
………………………
3.2.2. Собственные функции и собственные значения самосопряженных операторов.
1). Собственные значения эрмитовых операторов - вещественны.
Действительно,
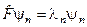 и
и 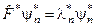 (3.2.6)
(3.2.6)
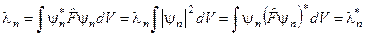
и получаем, что собственные значения эрмитовых операторов вещественны:
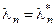 (3.2.7)
(3.2.7)
2) Произведение двух эрмитовых коммутирующих операторов есть эрмитов оператор
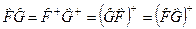 (3.2.8)
(3.2.8)
3) Важное свойство: пусть имеем дискретный набор собственных значений и собственных функций оператора 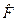 (считаем, что нет вырождения, т.е. волновые функции
(считаем, что нет вырождения, т.е. волновые функции 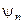 все разные для разных
все разные для разных 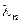 ):
):
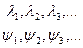 (3.2.9)
(3.2.9)
Такой набор волновых функций образует, так называемую, полную систему ортонормированных волновых функций:
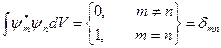 (3.2.10)
(3.2.10)
В самом деле, рассмотрим два равенства
…………………..
Вывод: условие ортонормированности собственных функций линейных самосопряженных операторов выполняется всегда. При наличии вырождения можно заменить собственные функции их ортонормированными линейными комбинациями.
4). Разложение в ряд по системе собственных функций линейных самосопряженных операторов.
Любую функцию можно представить
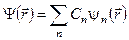
.................
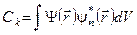
5). Вычисление средних значений.
Поскольку 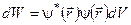 - вероятность найти частицу в элементе объема dV, то можно определить средние значения.
- вероятность найти частицу в элементе объема dV, то можно определить средние значения.
..................
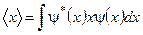
Дата добавления: 2015-08-08; просмотров: 4008;
