Операторы. Собственные функции и собственные значения.

АТОМНАЯ ФИЗИКА. ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ.

Глава 3. Элементы квантовой механики

Операторы. Собственные функции и собственные значения.

Операторы в квантовой механике.

Рассмотрим теперь еще одну возможную интерпретацию уравнений (в 4) и (в 5).

Когда волновая функция 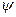известна, соответствующий импульс частицы или его 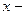компоненту 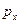мы получаем, взяв частную производную от волновой функции 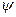по :

.

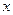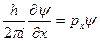Принято говорить, что 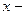компоненте импульса отвечает дифференциальный оператор

.

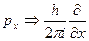Аналогичное утверждение справедливо и для 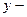и 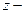компонент.

Соответственно, оператор, отвечающий энергии, имеет вид

.

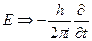Операторы, или правила, по которым производятся действия над какими-либо функциями (действуя на одну функцию, они порождают другую), можно представлять различными способами. Матрицы Гейзенберга являются одним определенным способом представления операторов. Другим представлением служит набор дифференциальных коэффициентов (операций дифференцирования), соответствующих компонентам импульса и энергии.

В квантовой механике любой динамической переменной, любой физической величине приводится в соответствие оператор.

Т.о., оператор 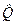– это правило, по которому любой выбранной функции 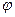приводится в соответствие другая функция :

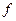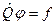(3.1.1)

Операциям возведения в степень, однократного и многократного дифференцирования, умножения на некоторую функцию и т.д. можно сопоставить соответствующие операторы. Примерами операторов могут служить ранее встречавшиеся .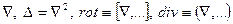

Оператор пишется всегда слева и действует на функцию, которая стоит справа от него.

Оператор действует на все, что стоит справа от него (если нет скобок).

Линейные операторы.

В квантовой механике применяются линейные операторы, чтобы не нарушался принцип суперпозиции состояний. Свойство линейных операторов:

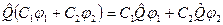(1.2)

где С₁, С₂ - произвольные постоянные.

Примерами линейных операторов могут служить единичный оператор: 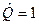, оператор умножения на число : .

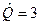Среди операторов, действующих на волновые функции 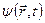, связанные (ассоциированные) с частицей, можно выделить два особенно важных типа линейных операторов:

1. операторы вида 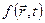, действие которых состоит в умножении волновой функции 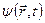на функцию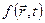

2. дифференциальные операторы .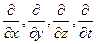

Напротив, оператор, сопоставляющий некоторой функции её куб, не является линейным оператором.

Используя линейные операторы, можно получить другие линейные операторы с помощью алгебраических операций умножения оператора на постоянную величину, сложения операторов, умножения операторов.

Примеры:

1) оператор координаты – оператор умножения: ;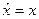

2) оператор проекции импульса – дифференциальный оператор: ;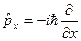

3) оператор полной энергии – гамильтониан: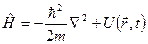

4) типичным примером линейного оператора, полученного путем умножения и суммирования линейных операторов, является оператор Лапласа:

.

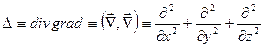Можно ввести и другие операторы, например, момента импульса, проекции момента импульса, спина и т.д.

Собственные функции и собственные значения.

Итак, каждой физической величине сопоставляется линейный оператор 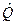, который, действуя на волновую функцию 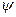, зависящую от координат 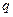, переводит её в другую функцию .

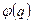Если оператор 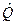воспроизводит функцию 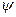с точностью до множителя

,

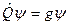то функцию 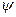называют собственной функцией оператора 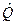, а множитель 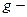собственным значением оператора .

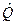Т.о., значения, которые может принимать физическая величина, называют в квантовой механике её собственными значениями, а об их совокупности говорят как о спектре собственных значений данной величины.

В классической механике величины пробегают, вообще говоря, непрерывный ряд значений.

В квантовой механике тоже существуют физические величины (примером могут служить координаты), собственные значения которых заполняют непрерывный ряд. В таком случае говорят о непрерывном спектре собственных значений.

Однако в квантовой механике, наряду с такими величинами, существуют и другие, собственные значения которых образуют дискретный набор. Это означает, что спектр собственных значений дискретный.

Т.о., спектр собственных значений может быть дискретным, сплошным (непрерывным) или смешанным.

Если спектр дискретный, то собственные значения и собственные функции можно пронумеровать

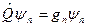(1.)

где n - немой значок, соответствующий номеру решения.

Физический смысл: собственные значения описывают в квантовой механике такие состояния, в которых данная физическая величина 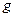имеет определенное значение .

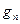Примеры.

1. Оператор координаты .

.

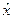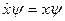Решение существует при всех 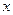, т.е. спектр собственных значений непрерывный.

1. Оператор проекции импульса.

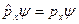
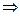
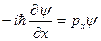
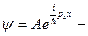собственная функция оператора импульса.

Очевидно, что спектр собственных значений оператора импульса непрерывный, поскольку имеем решения при всех значениях .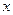

1. Оператор энергии – гамильтониан.

.

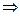
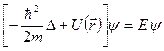В зависимости от потенциальной функции 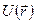система может иметь как дискретный спектр энергий (определенные уровни энергии), так и непрерывный.

Правила действия с операторами (алгебра операторов).

1. принцип суперпозиции.

;

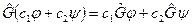2. свойство коммутативности

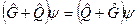
3. сложение операторов

;

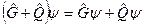4. умножение оператора на число эквивалентно умножению на это число результата действия оператора:

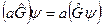
5. произведение линейных операторов обладает ассоциативным свойством:

;

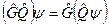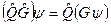
и свойством дистрибутивности:

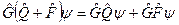
Однако!

В отличие от суммы, произведение двух операторов не коммутативно.

В этом состоит очень важное различие между алгеброй линейных операторов и алгеброй чисел. Произведение 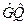не обязательно тождественно произведению 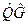. В первом случае сначала оператор 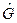действует на функцию 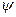, а затем оператор 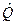действует на функцию 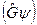и дает окончательный результат.

Во втором случае операци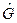и и 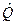переставлены между собой.

Разность 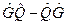двух произведений операторов называется коммутатором операторов 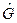и .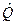

Коммутатор обозначается символом

.

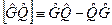Если указанная разность равна нулю, говорят, что операторы коммутируют

,

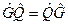и наоборот.

Примеры.

Рассмотрим совместное действие операторов, вычислив их коммутаторы.

1. координаты 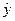и проекции импульса .

,

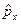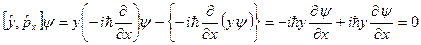т.е. 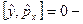операторы 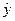и 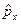коммутируют.

Коммутируют между собой все операторы дифференцирования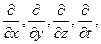

2. координаты 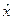и проекции импульса .

,

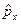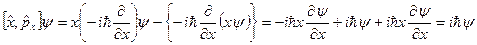т.е. 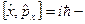операторы 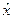и 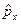не коммутируют.

Физический смысл:

физические величины, которым соответствуют некоммутирующие операторы, никогда не могут быть одновременно точно измерены – канонически сопряженные величины;

физические величины, чьи операторы коммутируют, могут быть одновременно точно измерены.