Соотношения неопределенностей Гейзенберга
В отличие от классических частиц, микрочастицы обладают волновыми свойствами, поэтому для них не всегда применимы такие классические понятия, как координата, импульс, время, энергия, траектория движения и т. д. В связи с этим возникают ограничения на применимость этих понятий при описании движения микрочастиц. Эти ограничения устанавливаются соотношениями неопределенностей Гейзенберга, согласно которым произведение неопределенностей (∆А, ∆В) двух сопряженных величин (А, В) не может быть меньше постоянной Планка 
:
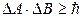
Сопряженными называют величины, которые не могут иметь одновременно точных значений. Сопряженными, например, являются координата микрочастиц и ее импульс, энергия частиц в квантовом состоянии и время жизни этой частицы в рассматриваемом состоянии. Для этих сопряженных величин соотношения неопределенностей Гейзенберга можно записать в виде:
,
, 
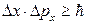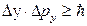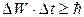,(8.9)
,
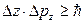где ∆х, ∆у, ∆z – неопределенности координат по осям х, у, z; ∆рх, ∆ру, ∆рz – неопределенности импульсов по осям х, у, z; ∆W– неопределенность энергии частицы в квантовом состоянии; ∆t – время жизни частицы в данном квантовом состоянии.
Чтобы убедиться в справедливости формул (8.9), рассмотрим пример прохождения электронов через щель шириной а(рис. 8.3). Если пропустить через щель большее число электронов, из-за наличия у них волновых свойств, на экране можно обнаружить дифракционную картину, состоящую, как и для света, из центрального максимума и очень слабых максимумов более высокого порядка.
|
При прохождении щели неопределенность координаты ∆х = а. Оценим ∆рх.Электрон, попадающий в минимум первого порядка, имеет проекцию импульса на ось хравную рх max.У разных электронов, попадающих в центральный максимум, рх изменяется от нулевого до максимального значения, ∆рх ~ рх max= psinφ1. А так как asinφ1= λ, то sinφ1= λ/a и ∆рх ≈р ∙(λ/a). Следовательно,
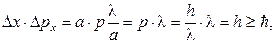
что и требовалось показать.
Согласно формуле
|
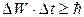
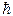/∆tосн= 0. В возбужденном состоянии атом может находится в течении времени tвозб≈1∙ 10-8 с, что приводит к размыванию по энергии возбужденного уровня энергии атома: ∆Wвозб≥ 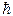/∆tвозб≠ 0. Поэтому излучаемые при переходе в основное состояние фотоны будет иметь разброс по частотам.
Используя соотношения неопределенностей, при рассмотрении движения микрочастицы, решается задача применимости классической механики. Классическая механика применима для описания движения микрочастиц, если можно пренебречьволновыми свойствами частицы, то есть длина волны де Бройля существенно меньше характерного размера установки. Например, электроны, движущиеся в электроннолучевой трубке, имеют длину волны де Бройля много меньшую поперечного размера трубки, в этом случае можно пользоваться законами классической физики. При движении электронов в атомах выполняется обратное соотношение, волновые свойства существенны, понятие траектории утрачивается.
Лекция 9
Дата добавления: 2015-08-08; просмотров: 748;