Волновые свойства микрочастиц. Принцип неопределенности Гейзенберга

На рис. 13.6 приведена схема мысленного эксперимента, поясняющего необычные свойства микрочастиц.

Рис. 13.6

Здесь пучок ускоренных электронов падает на экран с двумя узкими щелями. Если закрыть одну щель, то электроны, прошедшие через другую, рассеются так, как показано на рис. 13.7 а.

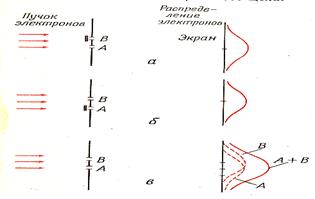
Рис. 13.7

Подобное же распределение, но несколько смещенное будет получено, если закрыть вторую щель и открыть первую (рис. 13.7 б)

Теперь оставим открытыми обе щели. Здравый смысл подсказывает, что новое распределение частиц должно равняться сумме первых двух (рис.13.7 в)

Однако опыт свидетельствует совсем о другом (рис.13.8).

Рис. 13.8

Распределение электронов отвечает интерференции двух когерентных волн!

Таким образом, на движение каждого отдельного электрона оказывают влияние обе щели!

Этот мысленный эксперимент подтверждает тот факт, что микрочастица-волна не просто «маленькое» материальное тело. Это объект, наделенный особыми свойствами, присущими элементам микромира.

Так, например, нельзя указать траекторию микрочастицы, измерить одновременно ее скорость и координату…

Рассмотрим еще один пример: дифракцию микрочастиц на щели.

Поток микрочастиц подлетает к экрану со щелью (рис.13.9). Пусть экран перпендикулярен потоку.

Рис. 13.9

Достоверно известно, что перед щелью х-компонента импульса микрочастицы P_x = 0. Здесь скорость частиц перпендикулярна экрану, т. е. оси x. Погрешность этого сведения ∆P_x = 0.

Но при этом совершенно не определена х-координата частицы.

Теперь рассмотрим движение частицы-волны в щели ∆х.

За щелью дифрагировавшие частицы будут отклонены в пределах угла ± φ.

Это максимальный угол, соответствующий дифракционному минимуму

Отклонение на угол φ означает, что у микрочастицы появилась х-компонента импульса

.

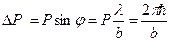Кроме того, теперь в щели мы можем указать х-координату с погрешностью

.

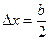Тогда 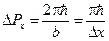или

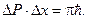
Последний результат обобщен Гейзенбергом и сформулирован как один из основных принципов квантовой механики.

Принцип неопределенностей Гейзенберга:

Произведение неопределенностей значений двух сопряженных переменных не может быть меньше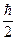

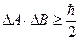(13.3)

Сопряженными величинами являются координаты и соответствующие проекции импульса, энергия и время. Произведение неопределенностей этих величин не может быть меньше по порядку величины постоянной Планка ħ т.е.

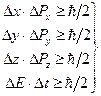(13.4)

Последнее соотношение означает, что чем точнее мы хотели бы померить энергию частицы, тем большее время займет это измерение.