Уравнение Шредингера. В 1926 году швейцарский физик Эрвин Шредингер записал в явном виде уравнение для волн волновой механики.
В 1926 году швейцарский физик Эрвин Шредингер записал в явном виде уравнение для волн волновой механики.
И сегодня до конца не ясно, как он нашел это уравнение.
Может быть, он рассуждал следующим образом.
Согласно гипотезе де-Бройля, каждой движущейся микрочастице должна быть сопоставлена волна.
Пусть свободной микрочастице, летящей вдоль оси x, соответствует плоская волна
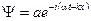 (13.5)
(13.5)
Свяжем параметры волны с энергией и импульсом микрочастицы
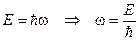
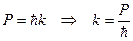
Теперь уравнение (13.5) можно записать иначе:
 (13.6)
(13.6)
Продифференцируем это выражение один раз по времени и дважды – по координате:
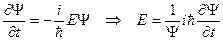 (13.7)
(13.7)
 (13.8)
(13.8)
В случае свободного движения нерелятивистской частицы, ее энергия и импульс связаны простым соотношением:

Теперь, принимая во внимание это соотношение, легко связать уравнения (13.7) и (13.8)
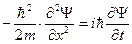 (13.9)
(13.9)
Это и есть волновое уравнение Шредингера для одномерного движения свободной частицы.
В случае движения микрочастицы в силовом поле, потенциальная энергия U, полная энергия E и импульс частицы связаны таким соотношением
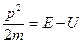
Объединяя в этом выражении уравнения (13.7) и (13.8), получим:
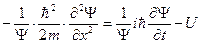
Или еще так
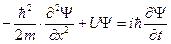 (13.10)
(13.10)
Это уравнение Шредингера для одномерного движения микрочастицы в силовом поле.
Для частицы, движущейся в произвольном направлении, запишем волновое уравнение в таком виде:
 (13.11)
(13.11)
Это уравнение получило название нестационарное волновое уравнение Шредингера.
Здесь: 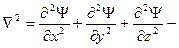 оператор Лапласа.
оператор Лапласа.
Таким образом
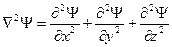
При движении микрочастицы в стационарном (неизменном во времени) силовом поле, решение уравнения Шредингера может быть представлено произведением двух множителей, один из которых является функцией только координат, а другой – только времени
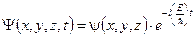 (13.12)
(13.12)
Используем это решение в дифференциальном уравнении (13.10)
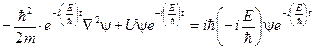 (13.13)
(13.13)
Сократив на общий множитель 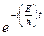 , получим уравнение Шредингера для стационарных состояний:
, получим уравнение Шредингера для стационарных состояний:
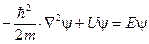 . (13.14)
. (13.14)
Это же уравнение можно представить еще и в таком виде:
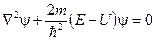 .
.
Дата добавления: 2015-08-04; просмотров: 1177;
