Туннельный эффект
Рассмотрим с позиций квантовой механики ещё одну задачу: задачу о преодолении частицей потенциального барьера высоты U0 (рис. 14.4). Частица, обладающая энергией E, движется вдоль оси x и встречает в точке x = 0 потенциальный барьер ширины l и высоты U0.
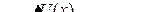
Рис. 14.4
Классическая механика предлагает два возможных сценария взаимодействия частицы с барьером.
1. Если E > U0, то частица просто минует барьер и продолжит движение в области ΙΙΙ.
2. Если E < U0, то частица отражается от барьера и движется далее в обратном направлении (-x). Область в этом случае для неё будет категорически недосягаемой. Рассмотрим теперь как взаимодействует с потенциальным барьером квантовая частица - волна.
Стационарное уравнение Шредингера
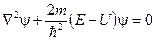
учитывая линейность нашей задачи, можно упростить и записать в следующем виде.
Для областей I и III, где U = 0
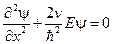(14.9)
А для области 0 ≤ x ≤ l, т.е. внутри барьера (U = U0)
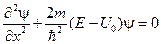(14.10)
Решение уравнений (14.9) и (14.10) подробно разобраны во многих пособиях (см. например [1]).
Мы ограничимся обсуждением конечного результата.
Решениями этих дифференциальных уравнений являются следующие функции.
Для области I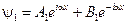 
Для области III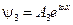 
Для области II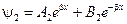 
Здесь постоянные α и β определяются высотой барьера U0 и параметрами частицы волны:
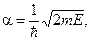
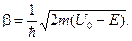
Приведенные решения означают что в областях I и II возможны как волны, распространяющиеся в положительном направлении (eiαx), так и в противоположном: (e-iαx, e-βx).
В зоне III, если там появляется частица волна, она распространяется только в положительном направлении оси x.
Отношение квадратов амплитуд отраженной волны (B1) и падающей (A1) называется коэффициентом отражения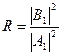 
.
Отношение квадратов амплитуд волн, прошедшей в область III (A3) и падающей на барьер (A1), называется коэффициентом прохождения или прозрачности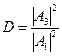 
.
Расчёт показывает, что коэффициент прохождения
.
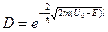Физический смысл коэффициента прозрачности (D) – вероятность прохождения частицы через потенциальный барьер из области I в область III. Эта вероятность не бывает нулевой даже когда энергия частицы E меньше высоты барьера U0.Квантовая частица в этом случае как бы «проникает сквозь барьер». Отсюда и название этого эффекта – туннельный эффект.
Интересно, что никогда не бывает равной нулю и вероятность отражения частицы-волна от барьера. Даже когда энергия (E) превышает уровень потенциального барьера (E > U0)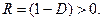 
Список литературы
1. Савельев И.В. Курс общей физики. Том 2, 3. – М.: «Наука», 2003.
2. Сивухин Д.В. Общий курс физики. Оптика. - М.: «Наука», 1980.
3. Э. Вихман. Квантовая физика. – М.: «Наука», 1977.
4. Макс Борн. Атомная физика. – М.: «Наука», 1968.
5. Трофимова Т.И. Курс физики. – М.: «Высшая школа», 1990.
6. Марио Льоцци. История физики. – М.: «Мир», 1970
Содержание
Лекция 1 «Общие представления о волновых процессах». 2
1. Введение. Волновые процессы.. 2
2. Гармонические колебания. 3
3. Скалярные и векторные волны.. 4
3.1. Кинематические характеристики плоской скалярной волны. 5
3.2. Геометрические типы гармонических волн. 7
4. Эффект Доплера. 8
5. Итог лекции 1. 9
Лекция 2 «Акустические волны». 11
1. Скорость звука в средах. 11
1.1. Продольные волны в твёрдом теле. 11
1.2. Упругая волна в идеальном газе. 12
2. Энергетические характеристики упругих волн. Вектор Умова. 15
3. Поведение продольной волны на границе двух сред. 17
Лекция 3 «Электромагнитные волны». 20
1. Уравнения Максвелла и их физический смысл. 20
2. Электромагнитные волны. Свойства электромагнитных волн. 21
3. Энергетические характеристики электромагнитных волн. Вектор Пойтинга. 23
4. Излучение электромагнитных волн. 24
4.1. Излучение точечного заряда. 24
4.2. Излучение элементарного вибратора (Диполь Герца) 25
4.3. Мощность излучения диполя. 26
4.4. Диаграмма направленности излучающего диполя. 27
Лекция 4 «Интерференция волн». 28
1. Суперпозиция двух сферических гармонических синфазных волн. 29
2. Особенности суперпозиции световых волн. Когерентность. 31
Лекция 5 «Интерференция световых волн». 34
1. Краткий обзор предыдущей лекции. 34
2. Сложение волн на «большом» расстоянии от источников. 35
3. Способы наблюдения интерференции света. 37
3.1. Зеркала Френеля 1816 г. 37
3.2. Бипризма Френеля. 38
3.3. Интерференционные полосы равной толщины (кольца Ньютона) 39
4. Итог лекции. 40
Лекция 6 «Интерференция волн». 41
1. Краткий обзор предыдущих лекций. Метод векторных диаграмм.. 41
2. Многолучевая интерференция. 41
3. Волновая область. Волновой параметр. 43
Лекция 7 «Дифракция волн». 46
1. Дифракция волн. Дифракция Френеля и дифракция Фраунгофера. 46
2. Принцип Гюйгенса-Френеля. 47
3. Метод векторных диаграмм. Зоны Френеля. 48
4. Дифракция от круглого отверстия. 51
5. Зонные пластинки. Фокусировка. 52
Лекция 8 «Дифракция волн». 54
1. Дифракция Фраунгофера от длинной щели. 54
2. Интенсивность дифракционной картины.. 57
3. Критерий типа дифракции. 59
Лекция 9 «Дифракционная решётка как спектральный прибор». 62
1. Краткий обзор предыдущих лекций. 62
1.1. Критерии типа дифракции. 62
1.2. Дифракция Фраунгофера от щели. 63
1.3. Многолучевая интерференция. 63
2. Дифракционная решётка как спектральный прибор. 64
3. Критерий Рэлея. Разрешающая сила дифракционной решётки. 65
Лекция 10 «Экспериментальные основы квантовой механики». 67
1. Равновесное теплового излучения. 67
1.1. Тепловое излучение абсолютно черного тела. 67
1.2. Классические теории Вина и Рэлея-Джинса.
«Ультрафиолетовая катастрофа». 69
1.3. Гипотеза Планка. 70
2. Фотоэффект. Уравнение Эйнштейна. 71
2.1. Опыты Столетова. 71
2.2. Эксперименты Ленарда и Томсона. 72
2.3. Уравнение Эйнштейна для внешнего фотоэффекта. 74
Лекция 11 «Экспериментальные основы квантовой теории». 77
1. Энергия и импульс фотона и релятивистской частицы.. 77
2. Эффект Комптона. 79
3. Корпускулярно-волновой дуализм излучения. 81
4. Задача. 83
Лекция 12 «Боровская теория атома водорода». 85
1. Модель атома Томпсона (1903) 85
2. Спектр атома водорода. 86
3. Опыт по рассеянию α-частиц. Планетарная модель атома Резерфорда. 87
4. Постулаты Бора (1913) 88
5. Опыт Франка и Герца (1914) 91
Лекция 13 «Волновые свойства микрочастиц». 93
1. Волновые свойства вещества. Гипотеза де-Бройля. 93
2. Экспериментальное подтверждение гипотезы де-Бройля. 94
2.1. Опыт Дэвиссона –Джермера (1926) 94
2.2. Волновые свойства микрочастиц. Принцип неопределенности Гейзенберга. 95
3. Уравнение Шредингера. 98
Лекция 14. «Уравнение Шредингера». 100
1. Уравнение Шредингера. Волновая функция и её физический смысл. 100
2. «Квантование как проблема собственных значений». 101
2.1. Частица в бесконечно глубокой одномерной потенциальной яме. 101
2.2. Туннельный эффект. 103
Список литературы ……………………………………………………………. 106
Содержание 107
Дата добавления: 2015-08-04; просмотров: 858;