Итог лекции 13

Уравнения Шредингера

1) Для одномерного движения свободной частицы (U = 0)

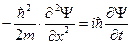
2) Для одномерного движения частицы в силовом поле

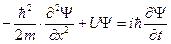
3) Нестационарное волновое уравнение

4) Стационарное волновое уравнение

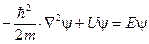
Мы познакомились с различными уравнениями движения микрочастиц – с волновыми уравнениями Шредингера. Но до сих пор остается не ясным: каково содержание самой Ψ – функции?

Рассматривая, например, акустическую волну, мы составляли волновое уравнение для давления или плотности среды. В волновом уравнении электромагнитной волны речь шла о напряженности электрического или магнитного полей…

Что же означает в уравнении Шредингера пси-функция (Ψ)? Каков ее физический смысл?

Этот вопрос мы подробно обсудим на следующей лекции.

Лекция 14. «Уравнение Шредингера»

План лекции:

1. Уравнение Шредингера. Волновая функция и её физический смысл.

2. «Квантование как проблема собственных значений».

2.1 Частица в бесконечно глубокой одномерной потенциальной яме.

2.2 Туннельный эффект.

1. Уравнение Шредингера. Волновая функция и её физический смысл

В самом начале 1923 года молодой французский физик Луи де Бройль опубликовал свою теорию волновой природы вещества. Основные положения теории были изложены в трёх его знаменитых докладах, предоставленных им Парижской Академии наук. Ключевым постулатом теории являлось предположение, что с каждой частицей с массой покоя m₀ связан волновой процесс с частотой ω₀.

При этом

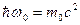
Здесь: ħ — постоянная Планка,

c — скорость света в пустоте.

Вскоре новая волновая механика получила неопровержимые экспериментальные подтверждения в работах Дависсона, Джермера, Томсона, Тартаковского, Фабриканта, и других исследователей.

Идея де Бройля привлекла внимание швейцарского физика Эрвина Шредингера. В 1926 году ему удалось в явном виде записать уравнение для волн волновой механики, т.е. для дебройлевских волн, связанных с материальными частицами

(14.1)

Важным отличием этого волнового уравнения от классических уравнений распространения различных волн состоит в присутствии мнимых коэффициентов в уравнении Шредингера. Эти мнимые коэффициенты принципиально неустранимы и в волновой ψ - функции.

Тем самым математически подтверждается тот факт, что волнам де Бройля, сопряженным с частицами, нельзя приписать «физического существования». Поэтому сам де Бройль называл эту волну «фиктивной», а Эйнштейн окрестил её «волной-призраком».

Но вскоре за этими волнами закрепилось другое название: «волны вероятности».

В 1927 годы Гейзенберг и Борн пришли к выводу, что квадрат модуля волновой функции в любой точке пространства и в любой момент времени есть мера того, что соответствующая частица находится в этой точке и в этот момент. Иными словами Борн и Гейзенберг предполагают существование частицы и связанной с ней непрерывной волны ψ, но частица не имеет ни определённой скорости, ни определённой траектории. Речь может идти лишь о вероятности нахождения частицы в той или иной области пространства. Эту вероятность и определяет волна ψ – функции - решение уравнения Шредингера.

Таким образом, вероятность dP обнаружить частицу в объёме dV можно записать в следующем виде

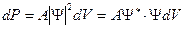(14.2)

Здесь: A — коэффициент пропорциональности.

Так как вероятность обнаружить частицу в пространстве равна единице («достоверное событие»), то

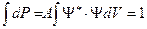
Обычно выбирают ψ - функцию так, чтобы A = 1, т.е.

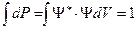
Этот интеграл представляет собой «условие нормировки».

Волновая функция (ψ), удовлетворяющая условию нормировки, называется нормированной функцией. Для нормированной ψ-функции

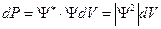(14.3)

В случае стационарного силового поля

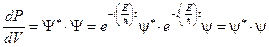
Это означает, что плотность вероятности обнаружить частицу в заданной точке стационарного поля, не меняется со временем:

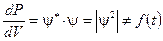(14.4)

Ещё раз отметим, что в волновой механике нет таких понятий классической механики как траектория, «точное» положение или «точная» скорость микрочастицы.

ψ-функция позволяет предсказать лишь вероятность обнаружения частицы в различных точках пространства.

На следующих двух примерах поясним, как решаются конкретные задачи о движение микрочастиц с помощью волнового уравнения Шредингера.

2. «Квантование как проблема собственных значений»

Именно такое название носит знаменитая работа Шредингера по волновой механике. Смысл этого названия состоит в следующем.

Так как ψ-функция связана с вероятностными характеристиками, эта функция должна быть однозначной, непрерывной, конечной и, кроме того, она должна иметь непрерывную и постоянную производную. Эти требования к ψ-функции получили название «стандартные условия».

Доказано, что уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям, не при любых значениях полной энергии частицы E. Эти значения энергии образуют ряд так называемых собственных значений.

ψ-функции, соответствующие этим собственным значениям энергии, называются собственными функциями.

Покажем, что волновое уравнение Шредингера автоматически приводит к дискретности энергии частицы и к энергетическим уровням.