Частица в бесконечно глубокой одномерной потенциальной яме

Рассмотрим, какие энергии доступны частице, помещённой в ящик длиной a с бесконечно высокими стенками (рис. 14.1). Здесь частице позволено двигаться вдоль оси x на участке от x = 0 до x = a. Потенциальная энергия частицы внутри ящика равна 0 при 0 ≤ x ≤ a и бесконечна за пределами потенциальной ямы когда x < a и x > a. Воспользуемся стационарным уравнением Шредингера:

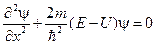(14.5)

Рис. 14.1.

Так как частица не может оказаться за пределами ямы (вероятность такого события равна 0), то ψ-функция вне ямы и на её границе равна нулю:

ψ(0) = ψ(l) = 0

Для частицы внутри потенциальной ямы, где U = 0, волновое уравнение принимает следующий вид:

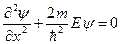(14.6)

Подобное дифференциальное уравнение хорошо известно из теории колебаний. Его решение

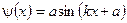, где

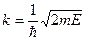
Выясним значение констант k и a, воспользовавшись граничными условиями. При x = 0

ψ (0) = a sina = 0.

Это означает, что a = 0.

Воспользуемся вторым граничным условием: при x = l,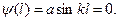

Отсюда следует, что .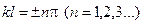

Вспомнив, что 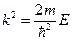, получим набор собственных значений энергии:

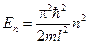. (14.7)

Так уравнение Шредингера ненасильственно приводит к дискретности энергии частицы в потенциальном ящике. Внутри потенциальной ямы частице доступны лишь вполне определённые значения энергии (рис. 14.2)

Рис. 14.2

Отыщем теперь собственные значения волновой функции .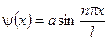

Здесь осталось определить только амплитуду, для чего воспользуемся условием нормировки:

.

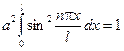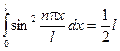, поэтому

Теперь собственные функции можно представить так

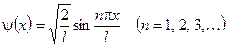(14.8)

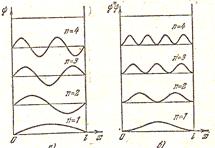
a) b)

Рис 14.3

Графики собственных функций (а) и плотности вероятности (b) приведены на рис.14.3. Попробуйте проанализировать полученные результаты.

Например, при n = 2 вероятность обнаружить частицу в центре ямы равна нулю, а при n = 1 эта вероятность максимальна!