Движение частицы в сферически симметричной прямоугольной потенциальной яме.
Развитие нанотехнологии инициировало широкое исследование новых классов нанообъектов, в частности квантовых точек, в которых осуществляется пространственное ограничение носителей заряда в трех измерениях. Квантовые точки как квазинульмерные системы важны не только как возможная элементная база для наноэлектроники, но и как модельные объекты для фундаментальных исследований. Электронный спектр изолированных КТ представляет собой набор дискретных уровней размерного квантования, и в этом смысле они могут рассматриваться как гигантские искусственные атомы с контролируемо изменяемыми параметрами, такими как глубина и характер удерживающего потенциала, число частиц и характерные размеры области их локализации.
Вид удерживающего потенциала определяется способом получения КТ. Для его представления наиболее часто используются модель «жестких стенок»и модель параболического удерживающего потенциала.
Соответствующая ортонормированная система одночастичных волновых функций имеет вид
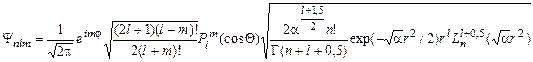(1.7.12)
где m-магнитное квантовое число; 
-присоединенные функции Лежандра первого рода; Г(x) - гамма-функция Эйлера; 
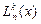- обобщенный многочлен Лагерра; r,Θ,φ- сферические координаты от центра ямы; α - параметр крутизны удерживающего потенциала U(r,Θ,φ)=αr2. Так как каждое значение 
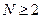может быть получено несколькими комбинациями значений n и l, стационарные состояния сферического осциллятора, начиная с третьего, оказываются g(N)-кратно вырожденными, причем
g(N)=0,5(N+1)(N+2) (1.7.13)
Например, уровень энергии 
будет шестикратно вырожден. В одном из этих шести состояний угловой момент (а следовательно, и орбитальное квантовое число l) равен нулю (s-состояние), а остальные пять состояний относятся к d-состояниям, которые различаются проекциями углового момента.
Необходимо отметить, что в случае сферического осциллятора вырождение каждого из p-, d-, f - и т.д. состояний является результатом сферической симметрии потенциального поля, а вырождение, благодаря которому s-состояние имеет энергию, совпадающую с энергией d-состояния (при N = 2), является «случайным». Оно обусловлено не симметрией задачи, а квадратичной зависимостью потенциальной энергии от радиуса. Если зависимость потенциальной энергии от радиуса будет отличаться от квадратичной (т.е. от U(r,Θ,φ)=αr2), например, членом βr2k, то вырождение, связанное со сферической симметрией, сохранится, а случайное - будет отсутствовать.
Дата добавления: 2015-08-11; просмотров: 1147;