Особенности движения частиц над потенциальной ямой.

Мы рассмотрели случай, когда полная энергия частицы Е меньше высоты стенок потенциальной ямы (финитное движение). Здесь размерный эффект проявляется в квантовании энергии и волнового вектора частицы.

Когда энергия частицы превосходит высоту стенок потенци­альной ямы (Е > U_j, см. рис. 1.4), движение частицы инфинитное.

Однако, здесь возможны отражение частиц от областей с резким изменени­ем потенциала (в данном случае от краев ямы) и даже своеоб­разный резонансный захват пролетающих над ямой частиц.

Если частица движется вдоль оси X, то, достигая потенциаль­ной ямы, она испытывает действие сил. При этом частица либо от­разится, либо «пройдет» над потенциальной ямой. В областях 1 и 2 (см. рис. 1.4, а) решение уравнения (1.1.2) имеет вид

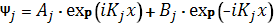(1.5.1)

где К₁ 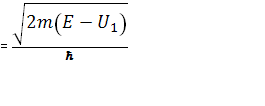, К₂

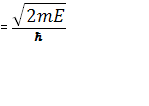
В области 3 (х > W/2) решение имеет вид уходящей от ямы волны

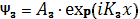(1.5.2)

здесь К₃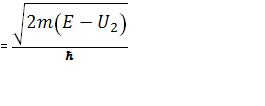

Чтобы вычислить коэффициенты прохождения и отражения (1.2.2), надо выразить амплитуды А₃ и В₁ через амплитуду падаю­щей волны A₁. Для этого используем условие непрерывности волно­вой функции и потока частиц при X = ±W/2. В результате получим

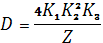(1.5.3)

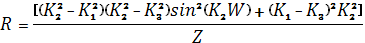
Z= 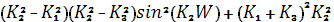(1.5.4)

Для симметричной ямы, когда К₁ = К₃ (см. рис. 1.4, б),

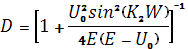(1.5.5)

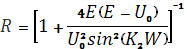(1.5.6)

Отметим, что по виду выражения (1.5.3) - (1.5.6) совпадают с аналогичными выражениями (1.3.2) - (1.3.5) для прохождения час­тицы над потенциальным барьером.

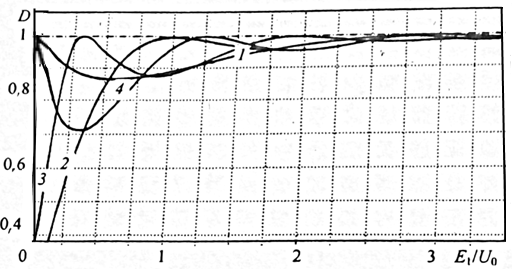
Согласно (1.5.3) при прохождении частиц над потенциаль­ной ямой, как и в случае потенциального барьера, коэффициент прохождения осциллирует с увеличением энергии частицы (рис. 1.7). В обоих случаях осцилляции имеют одну и ту же физи­ческую природу. Квазиклассически их можно трактовать как ре­зультат интерференции электронных волн, отраженных от скачков потенциала на границах барьера или ямы. Однако, при близком качественном характере за­висимостей имеются и заметные различия. Так, при равных значе­ниях ширин и скачков потенциала барьера и ямы размах осцил­ляции коэффициента D при прохождении частиц над чем при прохождении над ямой.

Рис. 1.7. Зависимость коэффициента прохождения частицы над потенциальной ямой от энергии: 1-U0/V=1, 2- U0/V=2, 3- U0/V=3, 4 - U0/V=4

На первый взгляд движение электронов над потенциальной ямой оказывается еще менее пригодным для наблюдения и исполь­зования осцилляции коэффициента прохождения частицы. Однако в данном случае заметные осцилляции могут наблюдаться при сравнительно небольших энергиях частицы, что улучшает условия их наблюдения.