Потенциальный барьер конечной ширины.

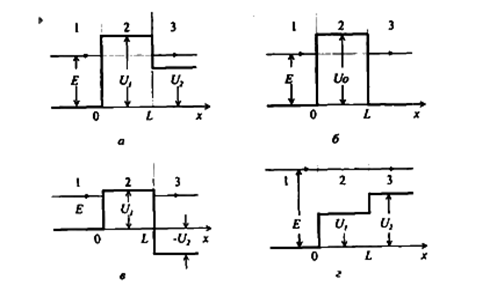
В реальной физической ситуации мы всегда имеем дело с барь­ером конечной ширины. Найдем коэффициенты отражения и про­хождения при движении частицы через прямоугольный потенци­альный барьер ширины I и высоты U₁ в предположении, что энер­гия частицы U₂<Е< U₁ (рис. 1 .2, а).

Используя результаты разд. 1.1, можем сразу записать решения уравнения Шредингера для трех областей (1, 2 и 3):

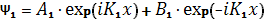
(1.2.1)

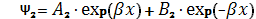
где К₁ , ,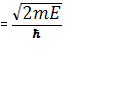

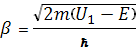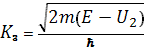
При записи уравнений (1.2.1) учтено, что в области 3 нет ис­точников частиц и рассеивающих центров, т.е. будет распростра­няться только прошедшая волна.

Подставив (1.2.1) в (1.1. 10) и (1.1. 11), получим

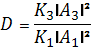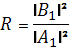, (1.2.2)

Амплитуды В₁ и A₃ найдем из системы линейных алгебраиче­ских уравнений, полученной с использованием условия непрерыв­ности волновой функции и ее первой производной на границе двух областей.

Так, при х = 0 имеем

А₁+В₁=А₂+В₂,

(1.2.3)

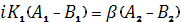
Рис. 1.2 Энергетическая диаграмма прямоугольного потенциального барьера

При x=L

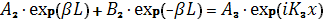
(1.2.4)

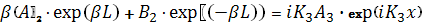
Решив систему уравнений (1.2.3), (1.2.4), для несимметричного барьера (рис. 1.2,а) получим

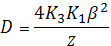, (1.2.5)

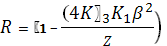(1.2.6)

Отсюда для случая симметричного барьера (рис 1.2 б), когда K₁=K₃, запишем

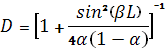(1.2.7)

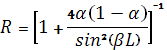(1.2.8)

Анализ выражений (1.2.5) и (1.2.7) показывает, что в случае барьера конечной ширины и высоты появляется конечная вероят­ность частице пройти под барьером, что абсолютно невозможно в классическом случае, так как при E<U₀ формально значение кине­тической энергии T становится отрицательным:

T = E-U₀<0.

Проникновение частицы с энергией E<U₀ через потенциальный барьер - чисто квантово-механический эффект, что видно из фор­мулы (1.2.5) (если положить в ней 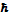=0, получаем D=0). Это явле­ние носит название туннельного эффекта.