Энергетическая диаграмма одномерной сверхрешётки

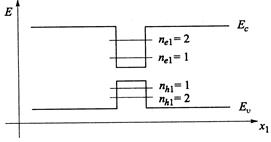
Полупроводниковые квантово-размерные структуры на основе гетеропереходов принято различать по числу направлений, вдоль которых происходит ограничение движения носителей заряда (электронов или дырок). Если их движение ограничено вдоль одного из направлений, например, вдоль оси х₁,то мы имеем дело с так называемой квантовой ямой. Для гетеропереходов 1-го типа такая структура изображена на рис. 1.3.

Рис. 1.3. Энергетическая диаграмма структуры с одиночной квантовой ямой. ne,h1 = 1,2... — квантовые числа нумерующие уровни размерного квантова­ния электронов и дырок. Заштрихованные области соответствуют областям непрерывных энергий.

Энергетический спектр носителей заряда в этом случае представляет собой двумерные подзоны:

,

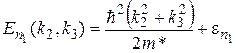где 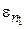— энергия размерного квантования.

Если движение носителей заряда ограничено вдоль двух направле­ний, например, вдоль осей х₁и х₂,то мы имеем дело с квантовыми проволоками (нитями), помещенными в матрицу широкозонного мате­риала. Энергетический спектр электронов и дырок в таких системах имеет вид одномерных подзон,

,

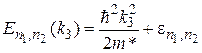с энергией размерного квантования 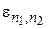. И, наконец, ограничение движения по всем трем направлениям х₁, х₂ и х₃ приводит к такому понятию как квантовая точка, помещенная в матрицу широкозонного материала. Энергетический спектр связанных состояний в квантовых точках является чисто дискретным .

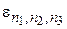Если квантовые ямы периодически продолжить вдоль направления, перпендикулярного интерфейсу, с периодом D, то мы приходим к новой квантово-размерной структуре — одномерной сверхрешетке (рис. 1.4).

Рис. 1.4. Энергетическая диаграмма одномерной сверхрешетки. Заштрихован­ные области соответствуют разрешенным значениям энергий для электронов и дырок.

Наличие барьеров конечной высоты и протяженности дает возмож­ность электронам и дыркам туннелировать из одной ямы в другую. В результате чего их дискретные уровни расщепляются в так называемые минизоны. Наличие трансляционной симметрии вдоль направления роста сверхрешетки (направление х₁)приводит к появлению дополни­тельного непрерывного квантового числа — сверхрешетчатого волно­вого вектора К₁(-p/D > K₁ ³ p/D). Таким образом, энергетический спектр носителей заряда в одномерной сверхрешетке будет состоять из чередующихся полос разрешенных и запрещенных энергий:

.

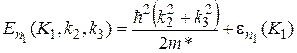Аналогичным образом могут быть созданы двумерные сверхрешет­ки из квантовых нитей и трехмерные сверхрешетки из квантовых точек. При определенных значениях параметров материалов возможна ситуация, когда один или оба носителя будут локализоваться в проме­жутках между нитями (антинити) или точками (антиточки), т. е. в мат­рице. Такие сверхрешетки можно назвать соответственно двумерными и трехмерными квантовыми сетями. В любом случае энергетический спектр носителей заряда в двумерных сверхрешетках будет опреде­ляться выражением

,

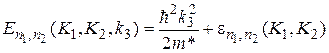а в трехмерных — 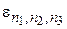(K₁, K₂, K₃). Здесь K — двумерный или трехмерный волновой вектор, характеризующий трансляционную сим­метрию соответствующих сверхрешеток.