Энергетическая диаграмма квантовой ямы с конечными стенками и дополнительным провалом.

В реальности мы имеем дело с потенциальными ямами, стенки которых имеют конечную высоту (см. рис. 1.9, а). Рассмотрим влияние конечной высоты стенок на разрешенные значения энер­гии основного и первого возбужденного состояний КЯ при нали­чии провала.

В этом случае необходимо дополнительно учесть возможность проникновения частицы под барьеры (т.е. в областях 4 и 5, см. рис. 1.9, а).Решение уравнения (1.8.1) для этих областей 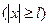можно записать в виде

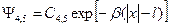(1.8.11)

где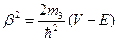

Учитывая граничные условия при x = ±d и x = ±l , можно было бы записать систему алгебраических уравнений, определяющую разрешенные значения K и E. Однако при этом пришлось бы ис­кать совместное решение системы из восьми уравнений. Для уп­рощения расчетов лучше учесть симметрию задачи и вместо гра­ничных условий для x < 0 использовать граничные условия при x = 0. При этом получим:

для четных состояний

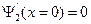(1.8.12)

для нечетных

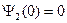(1.8.13)

Учитывая (1.7.12), (1.7.13) и граничные условия при x=d

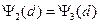
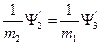(1.8.14)

и при x = l

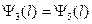
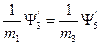(1.8.15)

получим две системы по пять уравнений, решения которых и опреде­лят разрешенные значения K и E длячетных и нечетных состоянии.

Соответствующие дисперсионные уравнения для определения разрешенных значений энергии и в этом случае (V≠∞) удается представить в виде (1.8.6) и (1.8.9), но уравнение для основного четного состояния теперь будет иметь вид

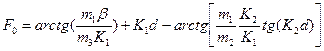(1.8.16)

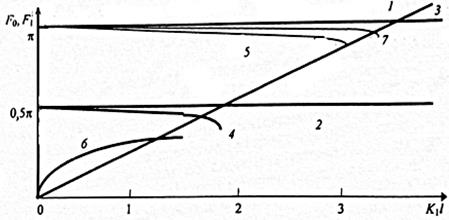
Рис. 1. 12. Графическое решение дисперсионных уравнений (1.8.6) и (1.8.9) с учетом (1.8.16) и (1.8.17): 1-K1l; 2,4,6-F0(K1l); 3,5, 7-F1 (K1l); 2,3-m2=m1, U=0, V=∞; 4,5- m2=m1, U=0, V≠∞; 6,7 - m2<m1, U≠0, V≠∞

а уравнение для первого возбужденного (нечетного) состояния может быть записано как

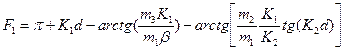(1.8.17)

Решение дисперсионных уравнений (1.8.6) и (1.8.9) с учетом (1.8.16) и (1.8.17) представлено на рис. 1.12.

Анализ показывает, что понижение высоты стенок КЯ уменьшает значения разрешенных уровней энергии как для ос­новного четного, так и для возбужденного состояния. Такому понижению способствует и увеличение т₃(эффективной массы материала барьеров). В результате условие существования основ­ного четного уровня в широкой части потенциальной ямы прини­мает вид

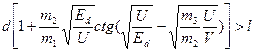(1.8.18)

Оценки [10] показывают, что, например, для структуры, у кото­рой барьеры изготовлены из А1Аs, широкая часть КЯ - из твердого раствора In_0.53Gа_0.47 Аs, провал - из InAs с параметрами V= 1,32 эВ, U=0,24эВ, d = 9,2 A, l=18,2 А, m₁= 0,046 m₀, т₂ = 0,023 m₀, m₃= 0,124m₀, уровни энергии основного и первого возбужденного состояний равны соответственно 0,09 и 1,22 эВ. В то же время для аналогичной структуры без провала эти же уровни соответствуют значениям 0,22 и 0,94 эВ. Таким образом, наличие провала может изменять положение уровней на несколько десятых электрон-вольт.