Энергетические состояния в прямоугольной квантовой яме с бесконечными стенками и дополнительным провалом.
Возможность получения слоев с произвольным профилем изменения состава позволила для улучшения характеристик приборов использовать структуры с КЯ сложной формы. Так, для создания нового поколения резонансно-туннельных диодов и гетеролазеров с раздельным электронным и оптическим ограничением применяются структуры с прямоугольными КЯ, в центре которых имеется дополнительный провал (рис. 1 .9, а).
Рассмотрим влияние дополнительного провала на энергетический спектр КЯ с бесконечно высокими стенками (рис. 1.9, б). При анализе учтем, что провал получен изменением материала и, следовательно, в области провала 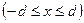 эффективная масса электрона m1 может отличаться от эффективной массы m2 в прилегающих областях
эффективная масса электрона m1 может отличаться от эффективной массы m2 в прилегающих областях 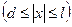 .
.
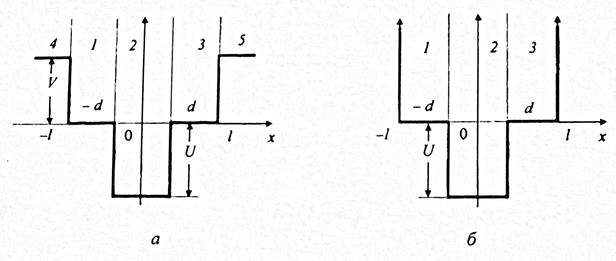
|
| Рис. 1.9. Энергетическая диаграмма квантовой ямы с конечными (а) и бесконечными (б) стенками и дополнительным потенциальным провалом |
В случае, когда эффективная масса зависит от координаты, одномерное уравнение Шредингера может быть представлено так:
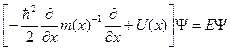 (1.8.1)
(1.8.1)
Для областей 1 и 3 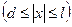 уравнение (1.8.1) принимает вид
уравнение (1.8.1) принимает вид

Аналогично для области 2 (  )имеем
)имеем
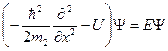
Найдем положение разрешенных энергетических уровней для E>0 (т.е. попадающих в широкую часть КЯ). В этом случае волновая функция во всех трех областях может быть представлена в виде
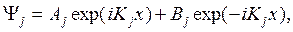
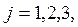
где
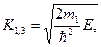
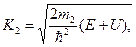
Для нахождения коэффициентов Aj и Bj , как обычно, воспользуемся условиями, обеспечивающими непрерывность волновой функции (непрерывность плотности частиц) и плотности потока частиц. Тогда при 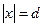 имеем
имеем
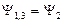
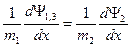 (1.8.2)
(1.8.2)
Кроме того, так как стенки КЯ бесконечно высокие, при 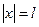
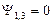 (1.8.3)
(1.8.3)
Используя граничные условия (1.8.2) и (1.8.3), получим два уравнения:
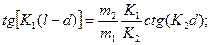 (1.8.4)
(1.8.4)
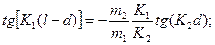 (1.8.5)
(1.8.5)
из которых первое определяет разрешенные K (а следовательно, и En) для четных состояний, а второе - для нечетных.
Анализ выражений (1.8.4) и (1.8.5) позволяет выявить влияние провала и различия эффективных масс на положение разрешенных уровней энергии.
Так, для основного (нижнего) четного состояния из (1.8.4) получаем
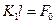 (1.8.6)
(1.8.6)
|
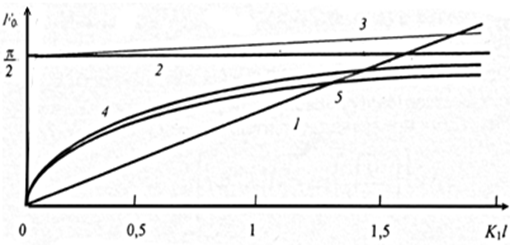
Рис. 1.10. Графическое решение уравнения (1.8.6):
1- 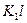 ; 2 – 5 - ; 2 – 5 - 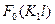 ; 2 – m2=m1, U=0; 3 - m2<m1, U=0; 4 - m2<m1, U≠0; 5 - m2=m1, U≠0 ; 2 – m2=m1, U=0; 3 - m2<m1, U=0; 4 - m2<m1, U≠0; 5 - m2=m1, U≠0
|
где
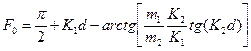 (1.8.7)
(1.8.7)
На рис. 1.10 представлено решение уравнения (1.8.6) графическим методом.
Разрешенные значения K1 при известной ширине КЯ (2l) определяются точками пересечения прямой 1 (соответствующей правой части уравнения (1.8.6)) с зависимостями 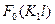 (кривые 2-5).
(кривые 2-5).
Анализ (1.8.6), (1.8.7) и приведенных зависимостей показывает, что для основного четного состояния: 1 - уменьшение эффективной массы m2 сдвигает разрешенный уровень энергии в область больших энергий; 2 - увеличение ширины d и глубины U провала понижает разрешенный уровень энергии; 3 - результирующее смещение уровня энергии определяется суперпозицией данных эффектов, при этом влияние эффективной массы обычно слабее. Так, при m2→0 аргумент arctg в (1.8.7) стремится к
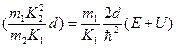
т.е. влияние т2 на решение уравнения (1.8.6) вообще исчезает, а влияние (d и U остается.
Увеличивая ширину и глубину провала, можно «затянуть» основной четный уровень из широкой части квантовой ямы в провал.
В этом случае кривые 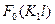 не будут пересекать прямую l (рис. 1.10) при
не будут пересекать прямую l (рис. 1.10) при 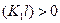 , а следовательно, производная функции
, а следовательно, производная функции 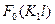 по переменной
по переменной  в точке
в точке 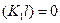 станет меньше единицы. Отсюда следует, что условие существования основного четного уровня в широкой части потенциальной ямы имеет вид
станет меньше единицы. Отсюда следует, что условие существования основного четного уровня в широкой части потенциальной ямы имеет вид
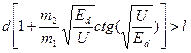 (1.8.8)
(1.8.8)
где

Анализ (1.8.8) показывает, что увеличение d, U, т1 или m2способствует втягиванию основного четного уровня в провал.
Рассмотрим теперь влияние параметров системы на положение первого возбужденного (нечетного) состояния. Как следует из (1.8.5), выражение для определения разрешенных значений K может быть представлено как
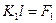 (1.8.9)
(1.8.9)
где
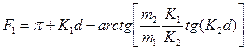 (1.8.10)
(1.8.10)
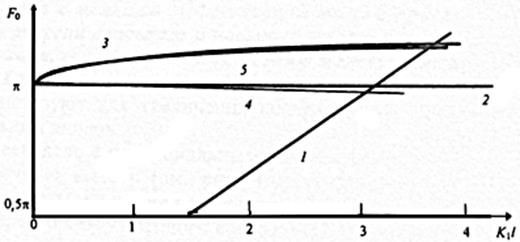
Решение уравнения (1.8.9) графическим методом показано на рис. 1.11.
|
Рис. 1.11. Графическое решение уравнения (1.8.9):
1- 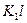 ; 2 – 5 - ; 2 – 5 -  ; 2 – m2=m1, U=0; 3 - m2<m1, U=0; 4 - m2=m1, U≠0; 5 - m2<m1, U≠0 ; 2 – m2=m1, U=0; 3 - m2<m1, U=0; 4 - m2=m1, U≠0; 5 - m2<m1, U≠0
|
Анализ показывает, что и в этом случае уменьшение т2 увеличивает разрешенное значение энергии, а рост d и U уменьшает, однако теперь ослабляется роль U.Так, устремляя m2к нулю, видим, что аргумент arctg в (1.8.10) стремится к
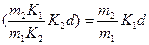
т.е. влияние U исчезает.
Различное влияние U и m2на положение основного и первого возбужденного состояний связано с различным видом волновых функций, соответствующих этим состояниям. Если для основного состояния в области провала велико значение 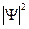 и мало значение
и мало значение 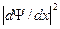 , то для первого возбужденного, наоборот, велико
, то для первого возбужденного, наоборот, велико 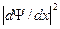 , но мало
, но мало 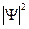 . Так как средняя энергия в данном состоянии
. Так как средняя энергия в данном состоянии
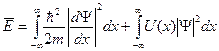
то оказывается, что в основном состоянии средняя энергия будет более «чувствительна» к наличию и величине провала, а в первом возбужденном состоянии - к значению m2.
В результате оказывается, что можно создать структуру, у которой наличие слоя с меньшей эффективной массой приведет к понижению энергии основного и повышению энергии возбужденного состояния, т.е. энергетический зазор между этими уровнями станет больше, чем в случае простой квантовой ямы, что, например, используют для увеличения контрастности ВАХ резонансно-туннельных диодов.
Дата добавления: 2015-08-11; просмотров: 883;
