Прохождение частицы через многобарьерные квантовые структуры.

При исследовании поведения частицы (электрона) в системах, содержащих изолированные КЯ и потенциальные барьеры, уста­новлено, что при туннелировании через одиночный потенциаль­ный барьер коэффициент прохождения D всегда будет меньше единицы. Казалось бы, что при туннелировании через два и более потенциальных барьеров общий коэффициент прохождения должен стать еще меньше. Однако это не всегда так и в ряде случаев ко­эффициент прохождения через многобарьерную систему может стать больше коэффициента прохождения через любой барьер этой системы. Данный эффект связан с интерференцией волн де Бройля и также может служить примером проявления размерных эффектов.

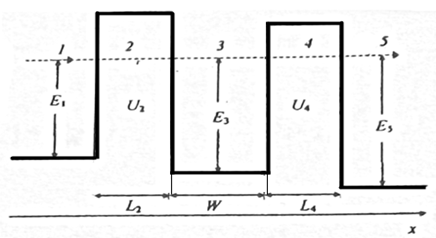
Рис. 1.18. Энергетический профиль двухбарьерной квантовой структуры.

Рассмотрим прохождение частицы через систему из двух потенциальных барьеров (рис. 1.18). Будем полагать, что потенциальная энергия системы не зависит от времени. Тогда состояния движения частицы через эту систему могут быть найдены из решения одно­мерного уравнения Шредингера (1.1.2). Для энергий, соответст­вующих туннелированию частицы через оба барьера, решения (1 . 1 .2) в областях 1,3 и 5 можно записать в виде

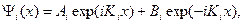
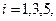(1.10.1)

Здесь 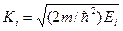(полагаем, что масса частицы во всех областях одинакова).

Для областей 2 и 4

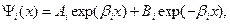(1.10.2)

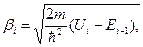
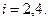
Подставляя (1.10.1) и (1.10.2) в (1.1.10), коэффициент прохож­дения D представим в виде

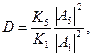(1.10.3)

Используя в качестве граничных условий равенства волновых функций и их первых производных на каждой границе, с учетом (1.10.3) получим

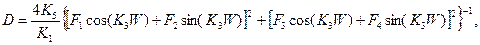(1.10.4)

где

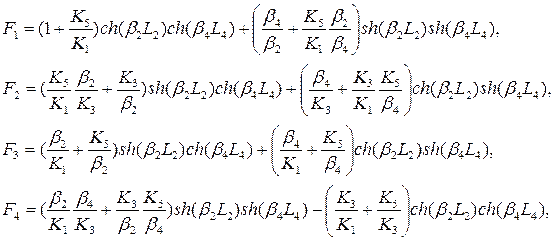
(1.10.5)

Аналогично можно получить выражение для расчета коэффи­циента прохождения двухбарьерной структуры, если энергия час­тицы соответствует интервалу, в котором частица проходит под первым барьером, но над вторым. Тогда коэффициент прохожде­ния удается представить в виде (1.10.4), где

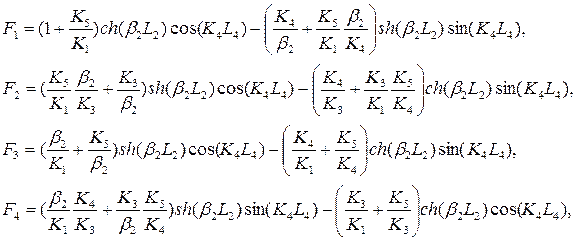
(1.10.6)

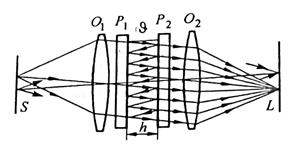
Отметим, что (1.10.4) соответствует выражению для расчета прохождения электромагнитных волн через интерферометр Фабри-Перро (рис. 1.19). Причем из геометрической оптики известно, что если волна, отразившись от пластины Р₂, приходит на поверхность пластины Р₁ с изменением фазы на 2πN, где N - целое число полуволн, то происходит усиление прошедшей волны вследствие интерференции со следующей приходящей волной. Это озна­чает, что для некоторых длин волн, определяемых расстоя­нием между пластинами, коэффициент прозрачности системы равен единице.

В случае симметричной двухбарьерной структуры, когда Е₁=E₃=E₅=E, U₂=U₄=U выражение (1.10.4) существенно упрощается и принимает вид

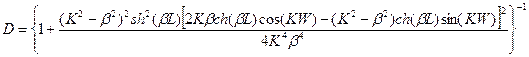(10.10.5)

где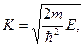

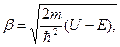
Рис. 1.19. Схема интерферометра Фабри-Перро: S- источник света, О1иО2- линзы, P1 и P2 - плоские пластины, ə- угол падения и отражения

Данное выражение соответствует формуле Эйри. Анализ (1.10.7) показывает, что в случае симметричной двухбарьерной квантовой структуры (ДБКС) коэффициент прохождения оказывается равным единице, если

(1.10.6)

здесь . Это выражение определяет значения энергии час­тицы, для которых наступает «резонансное» прохождение ДБКС и отражение полностью отсутствует.

Как уже отмечалось, этот эффект является следствием интер­ференции волн де Бройля, отражающихся от каждой границы раз­дела. Конечно, для полного подавления отражения от структуры (R = 0, D = 1) необходимо выполнение определенных фазовых и амплитудных соотношений для интерферирующих волн. При этом фазовые соотношения определяются энергией частицы и геометриче­скими размерами барьеров и КЯ, а амплитудные - отношением Е/U₀ .

Состояния в КЯ, соответствующие значениям энергии, для ко­торых D = 1, называют резонансными, а когда нужно подчеркнуть возможность ухода частицы из КЯ туннелированием через барье­ры, их еще называют квазистационарными или метастабильными. Энергетическое положение квазистационарных состояний оп­ределяется шириной КЯ и высотой барьеров. Зависимость же их энергетического положения от толщины барьеров L слабая. Тол­щина барьеров, в первую очередь, определяет «ширину» квазиста­ционарных уровней, связанную с конечной вероятностью ухода частицы из КЯ.

Полагая βL→∞, выражение (1.10.6) можно представить в виде (1.4.2). Таким образом, в случае непроницаемых барьеров уравнение (1.10.6) определяет энергетическое положение стационарных состояний в КЯ.

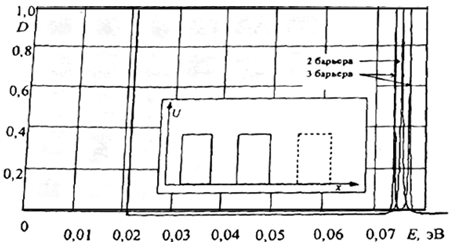
На рис. 1.20 представлена зависимость коэффициента прохо­ждения D от энергии для симметричной двухбарьерной кванто­вой структуры, рассчитанная по (1.10.7) с L = W = 3,0 нм, т = m₀ и U₀ = 0,1 эВ. Согласно расчетам в данном случае наблюдаются два резонансных пика, в максимуме которых D=1. Полуширина (ши­рина пика на полувысоте) первого пика меньше 0,1 мэВ, полушири­на второго пика - на порядок больше, что связано с повышением вероятности туннелирования частицы из КЯ при увеличении энер­гии частицы. Здесь же показана зависимость коэффициента прохо­ждения D от энергии частицы для трехбарьерной структуры при тех же параметрах ям и барьеров. В случае трехбарьерной структу­ры получить простое аналитическое выражение типа (1.10.7) не удается. Поэтому проводилось численное решение уравнения Шредингера с учетом «сшивания» волновых функций и их производных на шести границах.

Из рис. 1.20 видно, что в данном масштабе положение первого пи­ка для трех- и двухбарьерной структур совпало, а второй пик замет­но расщепился на два по обе стороны от пика, соответствующего двухбарьерной структуре.

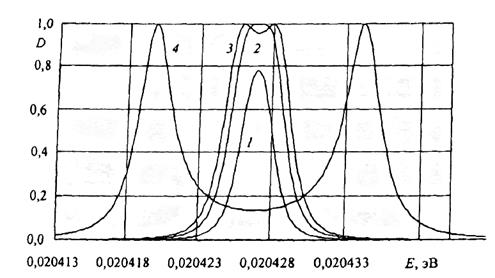
На рис. 1.21 в другом масштабе представлены зависимости D от энергии для первого пика трехбарьерной структуры при различ­ных значениях ширины среднего барьера (параметры внешних барьеров и квантовых ям соответствуют предыдущему случаю). Видно значительное влияние ширины среднего барьера на коэф­фициент прохождения. Согласно расчетам, при уменьшении тол­щины среднего барьера коэффициент D сначала возрастает, со­храняя форму резонансного пика, затем достигает единицы, когда толщина среднего барьера примерно в два раза больше толщин внешних барьеров, а затем расщепляется на два пика, которые удаляются друг от друга (отталкиваются) по мере уменьшения толщины среднего барьера.

Рис. 1.20. Зависимость коэффициента прохождения О через двух- и трехбарьерную структуры от энер­гии частицы; на вставке показан потенциальный профиль структуры

При этом провал между пиками углубляется. Та­кое поведение соответствует изменению дублетного расщепления в системе из КЯ, разделенных туннельно-прозрачным барьером. Заметим, что крайние пики на рис. 1.21 соответствуют первому пику на рис. 1.20. При этом из-за изменения масштаба расщепле­ние не проявляется (пики сливаются).

Когда энергия частицы превосходит высоту каждого из потенци­альных барьеров двухбарьерной квантовой структуры, приведенной на рис. 1.18 (Е≥U₂, U₄- надбарьерное прохождение), интерфе­ренция отраженных (от скачков потенциала) и падающих волн де Бройля будет приводить к немонотонной зависимости коэффициен­та прохождения от энергии частицы.

Рис. 1.21. Зависимости коэффициента прохождения D от энергии для трехбарьерной структуры: 1 - d = 2.5 dk, 2 - d = 2.15 dk, 3 - d = 1.9 dk, 4 - d = 1.5 dk, здесь d - ширина среднего барьера, dk -ширина внешних барьеров

Выражение для расчета коэф­фициента прохождения можно представить в виде (1.10.4) с

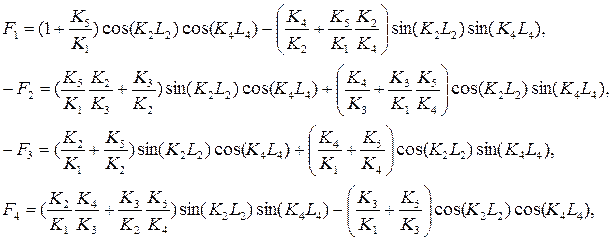
где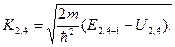

В случае симметричной двухбарьерной структуры, когда Е₁=E₃=E₅=E, U₂=U₄=U и L₂=L₄=L , выражение (1.10.4) при­нимает вид

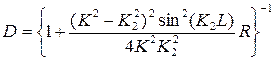(1.10.10)

где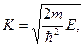

(1.10.11)

Согласно (1.10.10) при изменении энергии частицы коэффициент прохождения будет равен единице всякий раз, когда sin(К₂L) или R будут равняться нулю.

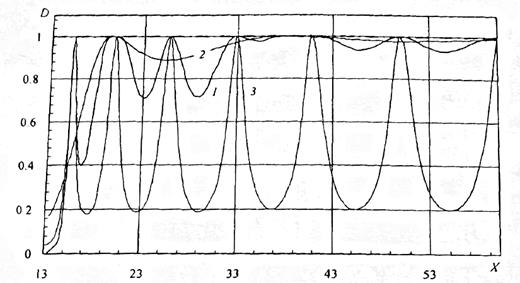
Зависимость коэффициента прохождения D от энергии части­цы, рассчитанная по (1.10.10), показана на рис. 1.22 (кривая 1).

Расчет проводился для L= 2 нм, W = 5 нм, m= 9.1∙10^-31 кг и U= 0.2 эВ . По оси х отложена энергия в относительных единицах X = Е/Е₀, где Е₀ - энергия первого уровня в БПЯ шириной W .

Рис. 1.22. Зависимость коэффициента прохождения D от энер­гии для симметричной двухбарьерной структуры (кривая 1); зависимость, рассчитанная по (1.10.10) при R = 1 (кривая 2); зависимость вида 1/(1 + R) (кривая 3)

Заметим, что при R = 1 (1.10.10) совпадает с выражением (1.3.4) для расчета коэффициента прохождения частицы над оди­ночным симметричным потенциальным барьером.

Таким образом, условие sin(К₂L) = 0 соответствует случаю, когда частица проходит над каждым барьером с коэффициентом прохождения, равным единице, и не возникает отраженных волн ни от первого, ни от второго барьера. При этом в области между барьерами концентрация частиц равна концентрации частиц с дан­ной энергией, испускаемых источником. Следовательно, частицы с данной энергией могут накапливаться только в области барьеров.

Согласно(1.10.11)условие R = 0 выполняется, если

(1.10.12)

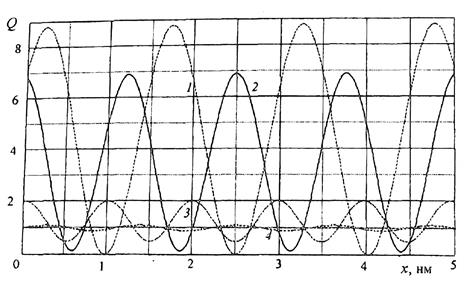
При этом коэффициент прохождения над каждым барьером по от­дельности не равен единице. Однако за счет накопления частиц в области между барьерами полный поток частиц, прошедших вто­рой барьер, будет равен потоку частиц, испускаемых источником, и будет подавлено отражение частиц, налетающих на первый барьер. На рис. 1.23 приведены зависимости распределения отношения концентрации частиц в окрестности точки х к концентрации частиц в падающей волне по межбарьерной области симметричной двух­барьерной структуры. При расчетах, как и ранее, полагали, что ширина барьеров L = 2 нм, ширина квантовой ямы W = 5 нм, вы­сота барьеров U₀ = 0,2 эВ (в относительных единицах 13,38).

Рис. 1.23. Распределение относительной концентрации частиц по межбарьерной области симметричной двухбарьерной структуры: для Х= 10,84; 15,5; 25,76; 20 (кривые 1-4 соответственно)

Кривая 1 на рис. 1.23 соответствует относительной энергии час­тицы X = 10,84 - энергии наивысшего (четвертого) квазистацио­нарного состояния в КЯ. При этом частица туннелирует под двумя барьерами. Амплитуда кривой 1 на рисунке уменьшена в 10 раз по сравнению с расчетной, т.е. в области между барьерами наблюда­ется существенное возрастание концентрации частиц.

Кривая 2 соответствует энергии частицы Х= 15,5 (первое надбарьерное резонансное состояние). Данная энергия отвечает усло­вию R = 0, т.е. (1.10.12). В области между барьерами также накап­ливаются частицы (Q > 1), однако значительно меньше, чем в первом случае. Такое поведение объясняется резким увеличением коэффициента прохождения области второго барьера с увеличени­ем энергии частицы при переходе от подбарьерного туннелирования к надбарьерному прохождению. В результате для создания одинаковых потоков частиц, прошедших через область второго барьера при подбарьерном туннелировании и надбарьерном про­хождении, в первом случае в области квантовой ямы необходимо накопить больше частиц (т.е. увеличить поток частиц, падающих на второй барьер), чем во втором.

Кривая 3 соответствует третьему надбарьерному резонансному состоянию с энергией X = 25,76. При данной энергии тоже выпол­няется условие R = 0 и в области между барьерами накапливаются частицы. Так как с увеличением энергии частицы коэффициент прохождения через область второго барьера возрастает, накопле­ние частиц становится еще менее выраженным.

Распределение относительной концентрации частиц с X = 20 по межбарьерной области симметричной двухбарьерной структуры по­казано кривой 4. Данная энергия почти соответствует энергии вто­рого надбарьерного резонансного состояния и условию К = 1. По­этому накопления частиц в этом случае практически не происходит.