Свойства непрерывных функций.
1. Сумма, произведение и частное двух непрерывных функций являются непрерывной функцией.
Док-во:
Докажем непрерывность суммы непрерывных функций.
Пусть f(x) и φ(x) непрерывны.
По первому определению непрерывности: 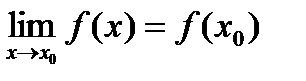 ,
, 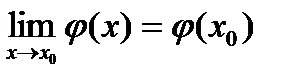 .
.
Рассмотрим 
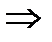 по первому определению сумма непрерывна в точке х0.
по первому определению сумма непрерывна в точке х0.
Непрерывность произведения и частного непрерывных функций доказывается аналогично.
Ч.т.д.
2. У непрерывной функции знак предела и знак функции можно менять местами.
Если f(x) ‒ непрерывная функция, то  .
.
Док-во: По первому определению непрерывности
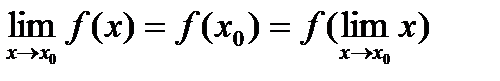 .
.
Ч.т.д.
3. Все элементарные функции непрерывны в своей области определения. y=xn, y=sin x, y=ex,…
Док-во:
а) y=const.
Возьмем произвольное значение х и дадим приращение Δx.
Тогда функция получит приращение:
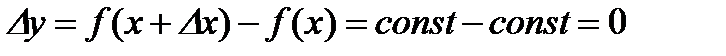 .
.
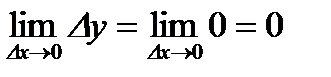 , т.к.
, т.к. 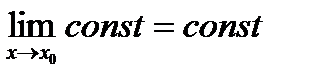 .
.
По второму определению непрерывности y=const непрерывна в своей области определения.
б) y=x.
Возьмем произвольное значение х и дадим приращение Δx.
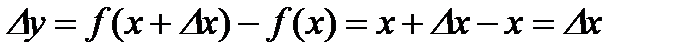 .
.
По второму определению непрерывности:
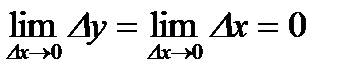 .
.
y=x непрерывна в своей области определения.
в) y=sinx.
Возьмем произвольное значение х и дадим приращение Δx.
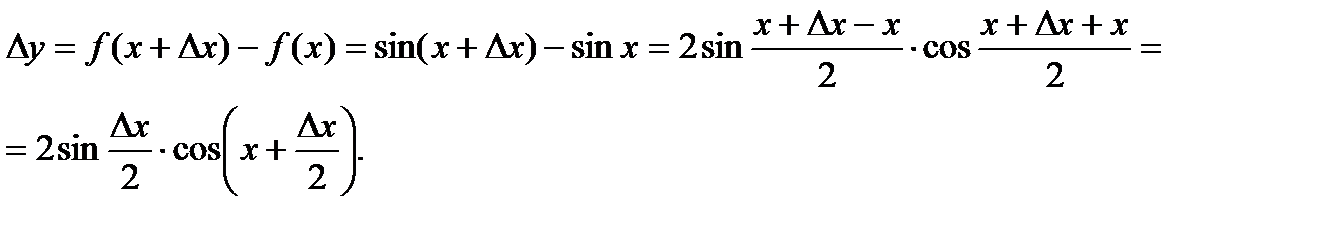
По второму определению непрерывности:
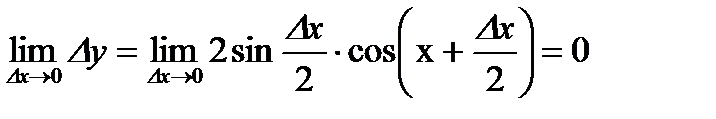
 0
0  cosx
cosx
как произведение б/м на ограниченную функцию.  y=sinx непрерывна при
y=sinx непрерывна при 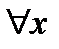 .
.
Ч.т.д.
4. Пусть функция x=x(t) непрерывна в точке t0. Пусть функция y=y(x) непрерывна в точке x0, где x0=x(t0) . Тогда сложная функция y=y(x(t)) непрерывна в точке t0.
Док-во:
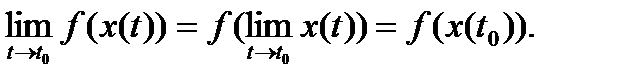
Тогда по первому определению сложная функция непрерывна в точке х0.
Ч.т.д.
Дата добавления: 2015-08-11; просмотров: 613;
