Глава 4. Предельные переходы в неравенствах. Замечательные пределы.

Теорема.Если функция 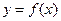неотрицательна в окрестности точки x₀, то и ее предел при x®x₀ тоже величине неотрицательная

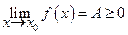. (3.9)

Доказательство ведем методом «от противного».

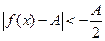Предположим, что A < 0, т.е. – A > 0. В определении предела подразумевается, что в качестве ε можно выбрать любое положительное число. Возьмем , по нему найдем зависящее от e положительное число d(e) > 0 такое, что для всех х, удовлетворяющих неравенству ½x₀ - х½< d, справедливо . Раскроем модульное неравенство

Рассмотрим правую часть неравенства и перенесем А направо. Получим

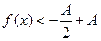
или

.

Это означает, что функция 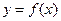отрицательна, что противоречит условию теоремы.

Следствие. Если f (x) < g (x), то и 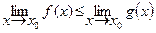. (3.10)