Первый замечательный предел

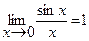. (3.11)

Построим тригонометрический круг с радиусом ОА = 1. Прямая DA – ось тангенсов. Возьмем на окружности точку В. Радиус ОВ = 1. Соединим точки А и В. Угол ВОА равен х, ВС = sin x, DA = tgx (рис. 4.1)

Предположим, что x > 0. Для x < 0 доказательство аналогично.,

Площадь треугольника ВОА

.

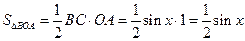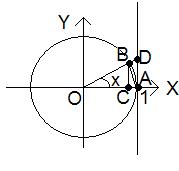
Рис. 4.1. Первый замечательный предел.

Площадь сектора ВОА

.

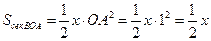Площадь треугольника DОА

.

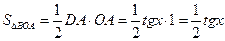Из чертежа следует, что для площадей выполняется соотношение

т.е.

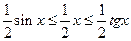
Сократим общий множитель ½ и разделим на sin (x). Получим

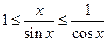
Или, для обратных величин

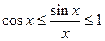
Так как 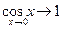, то и 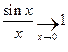. Что и требовалось доказать.

Следствие: 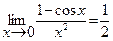(3.12)