Глава 5. Непрерывность функции. Односторонние пределы.

Функция f(x) называется непрерывнойв точке х₀, если она определена в этой точке и некоторой ее окрестности, а также

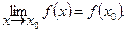(5.1)

Точки, в которых равенство (5.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка.

Обозначим за Dх разность между двумя значениями аргумента Dх = х₂ –х₁, а за Df (x) разность между двумя значениями функции Df(x) = f(x₂) - f(x₁). Тогда, если функция непрерывна, то бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если Dх® 0, то и Df (x) ® 0.

Введем понятие односторонних пределов. Число А называется пределом функции f(x) слева, если х®x₀ оставаясь все время меньше х₀ (x < x₀). Запись предела слева

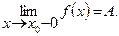
Аналогично вводится понятие предела справа, в этом случае х®x₀ оставаясь все время больше х₀ (x > x₀). Запись предела справа

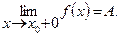
Для непрерывной функции предел слева совпадает с пределом справа и равен значению функции в точке х₀

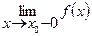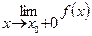= = f(x₀).

В точках разрыва цепочка равенств нарушается. Разрыв называется «разрывом первого рода», если все пределы конечны и «разрывом второго рода», если хотя бы один из пределов не существует или бесконечен.

Если хотя бы один из пределов равен бесконечности в точке х = х₀ , то говорят, что в этой точке есть вертикальная асимптота. Функция, имеющая на конечном промежутке конечное число разрывов первого рода называется кусочно непрерывной.

Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.

Пример 1. Найти точки разрыва функции.

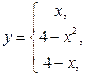если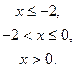

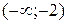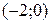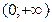Решение. На интервалах , и функция непрерывна. Проверке подлежат только точк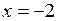и и .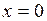

Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.

Рассмотрим точку .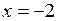

.

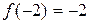Вычислим односторонние пределы

, .

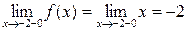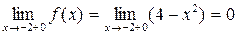Так как односторонние пределы не совпадают, 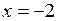- точка разрыва функции.

Рассмотрим точку .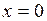

,

, ,

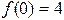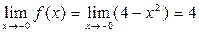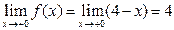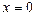- точка непрерывности функции, выполнены все условия непрерывности (рис. 5.1).

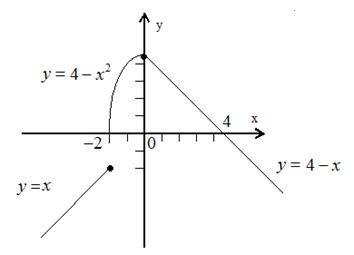
Рис. 5.1.

Пример 2. Исследовать поведение функции 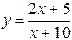вблизи точки разрыва. Построить схематический чертеж.

Решение. Область определения функции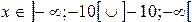

Точка разрыва 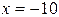. Найдем односторонние пределы

; .

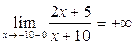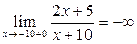Знак предела зависит от знаков числителя и знаменателя дроби. В обоих случаях числитель 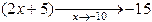, но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается положительным. Схематичный чертеж представлен на рис. 5.2.

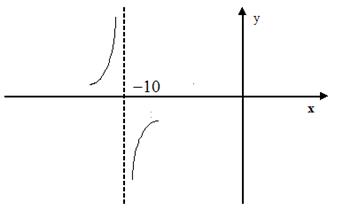
Рис. 5.2.