Глава 3. Правила вычисления пределов функции.
Теорема. Разность между функцией и ее пределом в точке х0 есть величина бесконечно малая, т. е., если 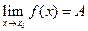 ,
,
то
f (x) = A + a (х) (3.1)
где a (х) бесконечно малая функция в окрестности точки х0.
Доказательство.Обозначим за a (х) разность между функцией и ее пределом
a (х) = f (x) – A.
Тогда из определения предела функции следует что, 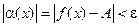 для всех х удовлетворяющих условию ½x0 - х½< d. Сравнив полученные соотношения с определением бесконечно малой функции, мы можем утверждать, что a (х) есть величина бесконечно малая.
для всех х удовлетворяющих условию ½x0 - х½< d. Сравнив полученные соотношения с определением бесконечно малой функции, мы можем утверждать, что a (х) есть величина бесконечно малая.
Справедливы следующие свойства пределов функций:
1. Если предел функции существует, то он единственен.
2. Предел постоянной величины С равен самой постоянной.
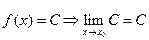 (3.2)
(3.2)
Если при х®x0 существуют конечные пределы функций f(x) и g(x)
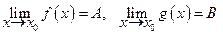 (3.3)
(3.3)
то справедливы следующие утверждения
3. 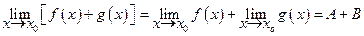 . (3.4)
. (3.4)
Действительно
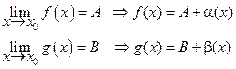
где α(х) и β (х) величины бесконечно малые. Так как сумма бесконечно малых есть величина бесконечно малая, т.е.
α(х) + β (х) = γ(х),
то
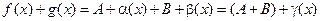 .
.
Отсюда следует, что 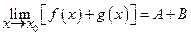
4. 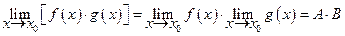 (3.5)
(3.5)
5. 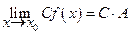 (3.6)
(3.6)
6. 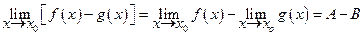 (3.7)
(3.7)
7. 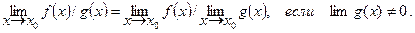 (3.8)
(3.8)
Пример 1. Вычислить 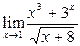 .
.
Решение. Так как
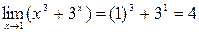 , а
, а 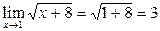 ,
,
то по теореме о пределе частного получаем, что 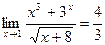 .
.
Как правило применять теоремы о пределах можно только после предварительного преобразования функций, стоящих под знаком предела. При этом возможны следующие неопределенные ситуации: 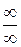 ,
, 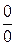 ,
, 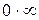 ,
, 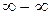 ,
, 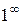 .
.
Приемом раскрытия неопределенности вида 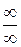 является деление числителя и знаменателя на наивысшую степень x.
является деление числителя и знаменателя на наивысшую степень x.
При неопределенности вида 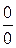 требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
требуется выполнить преобразование функции, выделив в числителе и знаменателе дроби множитель, стремящийся к нулю. Затем сократить дробь на этот общий множитель.
Неопределенности же вида 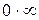 и
и 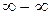 путем преобразований приводят к одному из рассмотренных случав
путем преобразований приводят к одному из рассмотренных случав 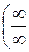 или
или 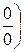 . Поясним сказанное на примерах.
. Поясним сказанное на примерах.
Пример 2. Вычислить 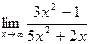 .
.
Решение. Наивысшая степень x вторая, делим числитель и знаменатель на 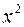 . Получим
. Получим
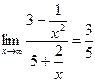 , так как
, так как 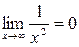 и
и 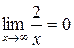 .
.
Дата добавления: 2015-08-26; просмотров: 948;
