Пример 3. Найти область определения функции .
Решение. Для существования функции 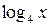 необходимо, чтобы
необходимо, чтобы 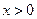 . Для существования функции
. Для существования функции 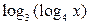 надо, чтобы
надо, чтобы 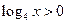 , откуда
, откуда 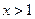 . Для существования функции
. Для существования функции 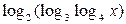 необходимо, чтобы
необходимо, чтобы  , откуда
, откуда 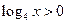 и
и 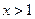 .
.
Таким образом, получены условия
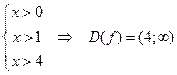 .
.
Пример 4. Найти область определения функции
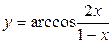 .
.
Решение. Так как 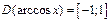 , то
, то
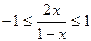 .
.
Решив неравенство, найдем область определения функции
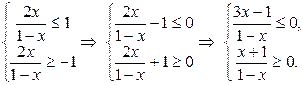
Применим метод интервалов (рис. 1.1)
| 1. | |
      1/3 1
1/3 1
| 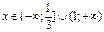 . .
|
| 2. | |
      -1 1
-1 1
|
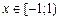 . .
|
| Рис. 1.1. |
Система неравенств имеет решение  .
.
Следовательно, 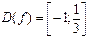 .
.
Пример 5. Определить, являются ли функции
1. 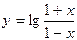 ;
;
2. 2. 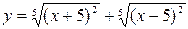 ;
;
3. 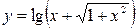 ;
;
4. 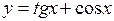
четными или нечетными.
Решение. Для определения свойств четности или нечетности функции следует проверить выполнение следующих положений:
1. Является ли область определение симметричной относительно начала координат, т.е. если 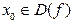 , то и
, то и 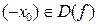 ;
;
3. Выполняются ли равенства 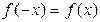 или
или 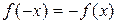 . При выполнении первого равенства функция окажется четной с графиком, симметричным относительно оси ординат, во втором – нечетной с графиком, симметричным относительно начала координат.
. При выполнении первого равенства функция окажется четной с графиком, симметричным относительно оси ординат, во втором – нечетной с графиком, симметричным относительно начала координат.
Для указанных в задаче функций:
-
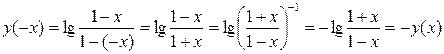 ,
,
то функция 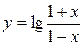 - нечетная;
- нечетная;
-
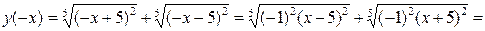
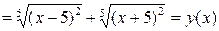 ,
,
то функция 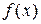 является четной;
является четной;
-

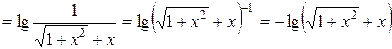 ,
,
следовательно, функция нечетная;
-
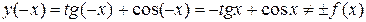 ,
,
следовательно, функция 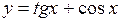 не является ни четной, ни нечетной.
не является ни четной, ни нечетной.
Пример 6. Найти период функции 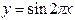 .
.
Дата добавления: 2015-08-26; просмотров: 790;
