Общее, базисное и частное решение систем линейных алгебраических уравнений.
Пусть 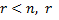 переменных
переменных 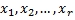 называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные
называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные 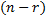 переменных называются неосновными (или свободными). Каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний
переменных называются неосновными (или свободными). Каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний 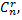 то и базисных решений имеется не более
то и базисных решений имеется не более 
Совместная система  линейных уравнений с
линейных уравнений с  переменными
переменными 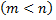 имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее
имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее 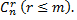
Достоинства метода Гаусса по сравнению с другими:
- менее трудоемкий метод;
- позволяет однозначно установить, совместна система или нет и в случае совместности найти ее решение;
- дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
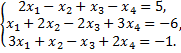
Составим расширенную матрицу по данной системе
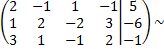
поменяем местами первую и вторую строку
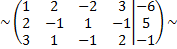
умножим первую строку на 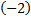 и сложим со второй строкой; умножим первую строку на
и сложим со второй строкой; умножим первую строку на 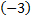 и сложим с третьей строкой
и сложим с третьей строкой
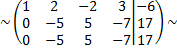
умножим вторую строку на 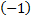 и сложим с третьей строкой
и сложим с третьей строкой
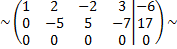
последняя строка вычеркивается, так как все ее элементы равны нулю
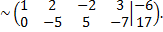
Ранг основной матрицы 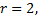 ранг расширенной матрицы
ранг расширенной матрицы 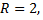 следовательно, система совместна. Число строк в основной матрице
следовательно, система совместна. Число строк в основной матрице 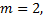 число столбцов в основной матрице
число столбцов в основной матрице 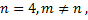 следовательно, система имеет множество решений.
следовательно, система имеет множество решений.
Выявим базисные переменные
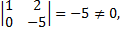
следовательно, 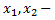 базисные переменные, тогда
базисные переменные, тогда
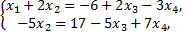
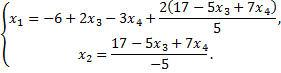
Дата добавления: 2015-08-11; просмотров: 3919;
