Линейные операции над векторами.
Линейными операциями над векторами называется сложение векторов и умножение вектора на число.
Суммой векторов является вектор 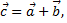 начало которого совпадает с началом вектора
начало которого совпадает с началом вектора 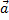 , а конец с концом вектора
, а конец с концом вектора 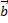 при условии, что начало вектора
при условии, что начало вектора 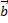 совпадает с концом вектора
совпадает с концом вектора 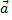 (правило треугольников).
(правило треугольников).
Каковы бы не были точки 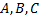 , имеет место векторное равенство
, имеет место векторное равенство
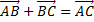 .
.

Рис. 4
Сложение векторов по правилу треугольников
Покажем сложение коллинеарных векторов с помощью параллельного переноса рис.5.
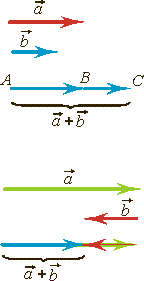
Рис.5
Если векторы 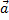 и
и 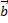 неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма векторов
неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. Диагональ параллелограмма есть сумма векторов 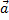 и
и 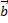
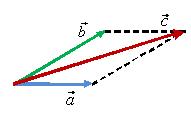
Рис. 6
Правило параллелограмма
Свойства сложения векторов.
Для любых векторов 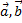 и
и 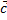 заданных в пространстве справедливы равенства:
заданных в пространстве справедливы равенства:
1) переместительный закон 
2) сочетательный закон 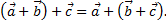
Произведением ненулевого вектора 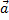 на число
на число 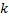 называется вектор
называется вектор 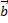 , длина которого равна
, длина которого равна 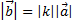 . Причем векторы
. Причем векторы 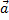 и
и 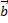 сонаправлены, если
сонаправлены, если 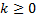 и противоположно направлены при
и противоположно направлены при 
Произведением нулевого вектора на любое число считается нулевой вектор.

Рис.7
Произведение вектора на число
Свойства умножения вектора на число.
Для любых векторов 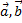 и любых чисел
и любых чисел 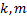 справедливы равенства:
справедливы равенства:
1) сочетательный закон 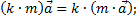
2) первый распределительный закон 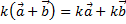 ;
;
3) второй распределительный закон 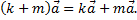
Любой вектор 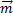 на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов
на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов 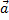 и
и 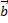

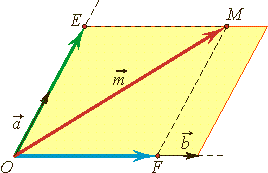
Рис.8
Базис вектора
Числа 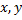 называются координатами вектора. Векторы
называются координатами вектора. Векторы 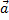 и
и 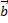 называются базисом вектора
называются базисом вектора 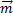 на плоскости.
на плоскости.
Базисом пространства называют любые три некомпланарных вектора, взятые в определенном порядке.
Любой вектор 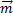 может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов
может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов 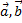 и
и 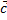
 .
.
Числа 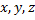 называют координатами вектора
называют координатами вектора 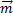 в данном базисе
в данном базисе 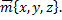
Дата добавления: 2015-08-11; просмотров: 1238;
