Линейное пространство

Очень часто приходится рассматривать некоторые множества объектов, для которых установлены линейные операции: сложение и умножение на число. Примером такого множества может служить множество свободных векторов, но и многие другие математические множества подчиняются линейным операциям. Например, множество всех функций непрерывных на отрезке, множество многочленов над некоторым полем.

При этом ни сами объекты не похожи на свободные векторы, ни линейные операции над этими объектами не похожи на линейные операции над векторами. Однако, во всех приведенных примерах есть нечто общее, позволяющее изучать линейные операции абстрактно, отвлекаясь от конкретной природы объектов.

Прежде всего, в приведенных примерах линейные операции над элементами данного множества дают в результате элементы того же множества: складывая элементы множества или умножая их на число, мы вновь получаем элементы того же множества.

Линейные операции, различные для разных множеств, имеют ряд общих свойств, что позволяет изучать линейные операции вообще.

Изучая множества с данными в них линейными операциями, их объединяют понятием линейного (векторного) пространства. Название пространства «векторное» проистекает из того, что это понятие было вначале выделено при изучении свободных векторов, которые представляют собой первый пример линейного пространства с внутренним законом геометрического сложения векторов и внешним законом умножения вектора на число. В силу этого элементы линейных пространств принято называть векторами, а сами линейные пространства часто называют векторными пространствами.

Определение линейного пространства обобщает определение совокупности всех векторов. Обобщение производится, во-первых, путем отвлечения от конкретной природы элементов множества с сохранением свойств действий над ними, во-вторых, путем отвлечения от конкретной природы допустимых множителей.

Пусть имеется множество L, состоящее из каких угодно элементов a,b,…,x,y,… Вместе с элементами множества L будем рассматривать действительные и комплексные числа 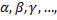образующие множество K.

Будем считать, что в множестве L определены действия сложения и умножения, если:

1) каждым двум элементам a и b из L сопоставлен некоторый элемент того же множества L, называемый их суммой. Сумма элементов a и b обозначается через ;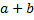

2) каждому числу и каждому элементу a из L сопоставлен некоторый элемент того же множества L, называемый произведением на a или a на , которое мы обозначим как или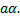

Линейным (векторным) пространством L над полем K, называется множество L рассматриваемое вместе с заданным в нем действиями сложения и умножения на число, удовлетворяющее следующим аксиомам:

1) для любых a и b из L

то есть операция сложения элементов из L обладает перестановочны (коммутативным) свойством:

2) для любых a,b,c из L

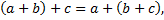
то есть операция сложения элементов из L обладает сочетательным свойством и позволяет писать сумму элементов без скобок;

3) в L существует такой элемент 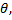что

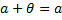
для любого a из L. Элемент