Линейные преобразования
Будем говорить, что на множестве векторов 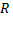 задано преобразование
задано преобразование 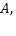 если каждому вектору
если каждому вектору 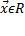 по некоторому правилу поставлен в соответствие вектор
по некоторому правилу поставлен в соответствие вектор 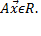
Преобразование  называется линейным, если для любых векторов
называется линейным, если для любых векторов  и
и 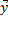 и для любого действительного числа
и для любого действительного числа  выполняются равенства
выполняются равенства 
Линейное преобразование называется тождественным, если оно преобразует любой вектор  в самого себя.
в самого себя.
Тождественное преобразование обозначается 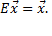
Рассмотрим трехмерное пространство с базисом 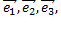 в котором задано линейное преобразование
в котором задано линейное преобразование 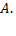 Применив его к базисным векторам, мы получим векторы
Применив его к базисным векторам, мы получим векторы 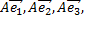 принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса
принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса
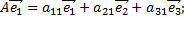
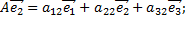
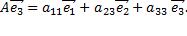
Матрица

называется матрицей линейного преобразования  в базисе
в базисе 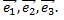 Столбцы этой матрицы составляются из коэффициентов в формулах преобразования базиса.
Столбцы этой матрицы составляются из коэффициентов в формулах преобразования базиса.
Матрицей тождественного преобразования является единичная матрица 
Для произвольного вектора 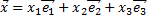 результатом применения к нему линейного преобразования
результатом применения к нему линейного преобразования  будет вектор
будет вектор 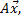 который можно разложить по векторам того же базиса
который можно разложить по векторам того же базиса 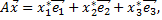 где координаты
где координаты 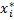 можно найти по формулам:
можно найти по формулам:
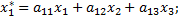
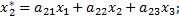
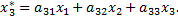
Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы 

Обратный переход от нового базиса 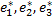
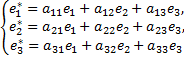
к старому базису  осуществляется с помощью обратной матрицы
осуществляется с помощью обратной матрицы 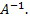
Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор 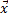 имеет координаты
имеет координаты 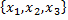 относительно старого базиса и координаты
относительно старого базиса и координаты 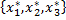 относительно нового базиса, т.е.
относительно нового базиса, т.е.
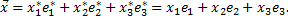
Подставив значения
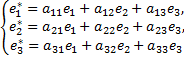
в левую часть равенства, получим после преобразований
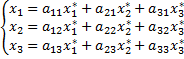
или в матричной форме
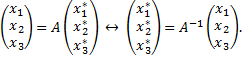
Рассмотрим пример. Вектор 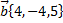 заданный в базисе
заданный в базисе 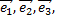 выразить в базисе
выразить в базисе
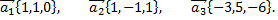
Выразим связь между базисами
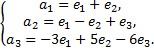
Матрица перехода от базиса 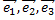 к базису
к базису 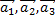 имеет вид
имеет вид
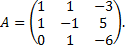
Найдем матрицу обратную данной
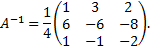
Согласно формуле
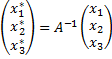
получим новые координаты вектора 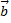 в базисе
в базисе 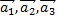
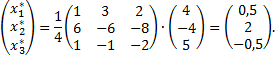
Таким образом, вектор 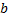 может быть представлен в виде
может быть представлен в виде
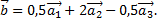
Дата добавления: 2015-08-11; просмотров: 1411;
