Свойства собственных векторов матрицы

Свойства собственных чисел и собственных векторов.

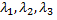1) Если выбрать базис из собственных векторов соответствующих собственным значениям матрицы 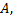то в этом базисе линейное преобразование имеет матрицу диагонального вида

2) Если собственные значения преобразования различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы имеет три различных корня, то в некотором базисе матрицы имеет диагональный вид.

Рассмотрим пример. Найдем собственные числа и собственные векторы матрицы

Составим характеристическое уравнение

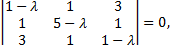
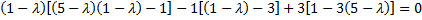
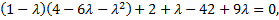
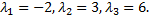
Найдем координаты собственных векторов, соответствующих каждому найденному значению 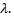Если собственный вектор, соответствующий то

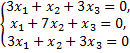
- совместная, но неопределенная система. Ее решение можно записать в виде

где 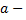любое число.

Если то получим систему для определения координат второго собственного вектора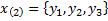

откуда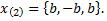

Для 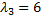найдем собственный вектор

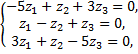
откуда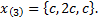

Следует заметить, что

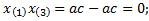
Вывод: собственные векторы этой матрицы попарно ортогональны.

Контрольные вопросы

1. Какая матрица называется матрицей линейного преобразования?

2. Как определить зависимость между координатами вектора в разных базисах?

3. Какой вектор называют собственным вектором матрицы?

4. Перечислить основные свойства собственных чисел и собственных векторов.