Свойства прямой в евклидовой геометрии.

1) Через любые две несовпадающие точки можно провести единственную прямую.

2) Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.

3) Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

Любая прямая на плоскости может быть задана уравнением первого порядка

,

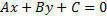причем, постоянные 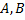не равны нулю одновременно, т.е.

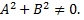
Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных 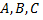возможны следующие частные случаи:

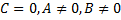- – прямая проходит через начало координат;

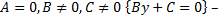- прямая параллельна оси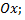

- – прямая параллельна оси

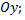
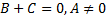- – прямая совпадает с осью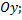

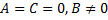- – прямая совпадает с осью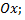

Уравнение прямой может быть представлено в различном виде, в зависимости от каких-либо заданных начальных условий.