Нормальное уравнение прямой.

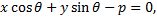
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси 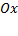и направлением этого перпендикуляра. Если 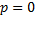, то прямая проходит через начало координат, а угол

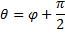
задаёт угол наклона прямой.

Вывод нормального уравнения прямой.

Пусть дана прямая ,тогда

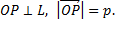
Рассмотрим для этого перпендикуляра его орт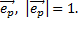

Допустим, что угол между 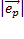и осью 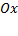равен 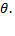Так как

,

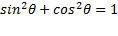то можно записать 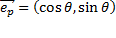. Теперь рассмотрим произвольную точку 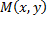. Проведем радиус-вектор 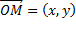, найдем проекцию 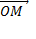на вектор .

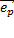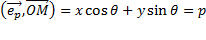
следовательно,

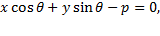
это и есть нормальное уравнение прямой.

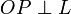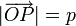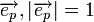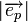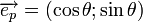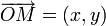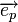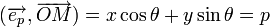Пусть дана прямая L. Тогда и . Рассмотрим для этого перпендикуляра его орт . Допустим что угол между и осью X равен θ. Так как , то можно записать: . Теперь рассмотрим произвольную точку . Проведем радиус-вектор Теперь найдем проекцию на вектор . следовательно: Это и есть нормальное уравнение прямой ■

Если прямая задана общим уравнением

,

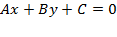то отрезки и , отсекаемые ею на осях, угловой коэффициент , расстояние прямой от начала координат , и 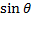выражаются через коэффициенты 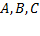следующим образом

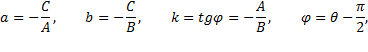
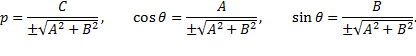
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие 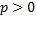. В этом случае и являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если 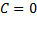, то прямая проходит через начало координат и выбор положительного направления произволен.

Уравнение прямой, проходящей через две заданные несовпадающие точк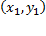и и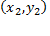

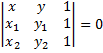
или

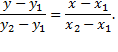
Векторно-параметрическое уравнение прямой задается вектором 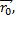конец которого лежит на прямой и направляющим вектором прямой . Параметр пробегает все действительные значения

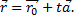
Параметрические уравнения прямой могут быть записаны в виде

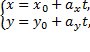
где — произвольный параметр, 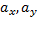— координаты и 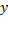направляющего вектора прямой, при этом

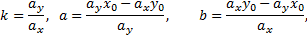
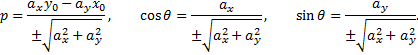
Смысл параметра аналогичен смыслу параметруа в векторно-параметрическом уравнении.

Каноническое уравнение получается из параметрических уравнений делением одного уравнения на другое

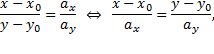
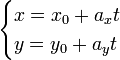
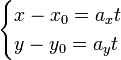
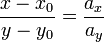
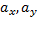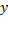где — координаты и направляющего вектора прямо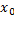й, и 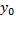координаты точки, принадлежащей прямой.