Угол между прямыми. Условия параллельности и перпендикулярности двух прямых

Угол 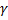между пересекающимися прямыми определяется по формуле

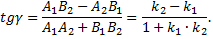
При этом под углом 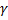понимается угол, на который надо повернуть первую прямую, заданную параметрами , вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.

Прямые параллельны, ес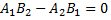ли или

Прямые перпендикулярны, ес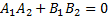ли или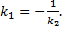

Любую прямую, параллельную 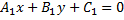, можно выразить уравнением 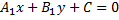, при этом расстояние между ними будет равно

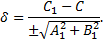
Если знак перед радикалом противоположен 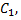то будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.

Для того, чтобы три прямые

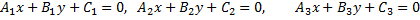
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие

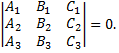
Если и 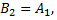то прямые

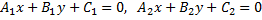
перпендикулярны.

Рассмотрим пример. Две прямые заданы уравнениями

найти угол между данными прямыми.

Так как

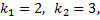
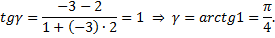
Рассмотрим пример. Задана прямая

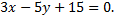
Составить для этой прямой уравнение в отрезках и при желании построить ее.

Преобразуем исходное уравнение прямой

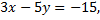
разделим обе части уравнения на (-15)

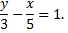
Прямая проходит через точк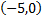и и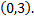

Контрольные вопросы

1. Дать определение уравнения линии на плоскости.

2. Перечислить и записать уравнения прямой линии. Пояснить геометрический смысл коэффициентов каждого уравнения.

3. Как найти угол между прямыми?

4. Назвать условия параллельности и перпендикулярности прямых.

5. Записать формулу нахождения расстояния от точки до прямой.