Каноническое уравнение окружности и ее основные характеристики
Кривые второго порядка описываются уравнениями второй степени с двумя переменными
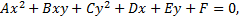
если по крайней мере одна из величин 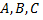 не равна нулю.
не равна нулю.
Окружность – это множество всех точек плоскости, равноудаленных от данной точки (центра). Если 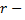 радиус окружности, а точка
радиус окружности, а точка 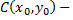 ее центр, то уравнение окружности имеет вид
ее центр, то уравнение окружности имеет вид
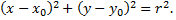
Если центр окружности совпадает с началом координат, то уравнение примет вид
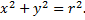

Рис. 11
Окружность с центром в начале координат
Взаимное расположение точки 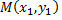 и окружности
и окружности 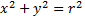 определяется условиями:
определяется условиями:
1) если 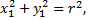 то точка
то точка 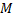 лежит на окружности;
лежит на окружности;
2) если  то точка
то точка  лежит внутри окружности;
лежит внутри окружности;
3) если  то точка
то точка 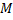 лежит вне окружности.
лежит вне окружности.
Рассмотрим пример. Найти координаты центра и радиус окружности 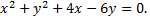
Приведем уравнение окружности к общему виду. Для этого сгруппируем слагаемые, содержащие переменную  и слагаемые, содержащие переменную
и слагаемые, содержащие переменную 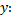

Выражения в каждой из скобок разложим до полного квадрата
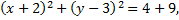
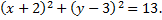
Таким образом, определяем координаты центра окружности и ее радиус
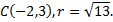
Рассмотрим пример. Составить уравнения касательных к окружности
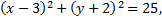
проведенных в точках пересечения окружности с прямой 
Найдем точки пересечения окружности и прямой, для чего решим систему уравнений
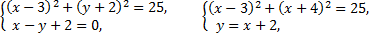
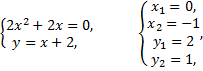
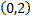 и
и 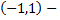 точки пересечения окружности и прямой.
точки пересечения окружности и прямой.
На координатной плоскости 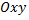 построим окружность и прямую.
построим окружность и прямую.
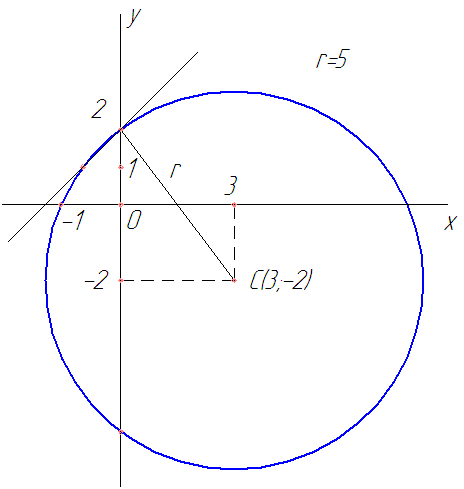
Рис. 12
Касательная к окружности
Запишем уравнение прямой, проходящей через точку 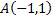
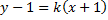
- это касательная к окружности, следовательно, она перпендикулярна радиусу 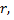 т.е. прямой
т.е. прямой 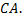 Запишем уравнение прямой
Запишем уравнение прямой 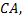 учитывая, что
учитывая, что 
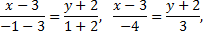
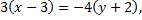
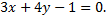
Получили искомое уравнение прямой 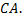 Запишем угловой коэффициент данной прямой
Запишем угловой коэффициент данной прямой
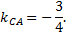
Прямая, проходящая через точку 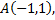 перпендикулярна прямой
перпендикулярна прямой 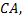 следовательно ее угловой коэффициент
следовательно ее угловой коэффициент
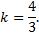
 Запишем полностью уравнение искомой прямой
Запишем полностью уравнение искомой прямой
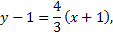
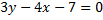
- это есть уравнение касательной, проходящей через точку 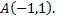
Найдем уравнение касательной в точке 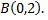 Запишем уравнение прямой
Запишем уравнение прямой  если
если 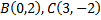
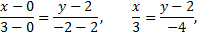
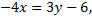
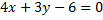
- уравнение прямой  Угловой коэффициент данной прямой равен
Угловой коэффициент данной прямой равен
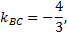
тогда

Уравнение искомой прямой находим в виде
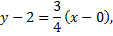
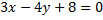
- это уравнение касательной в точке 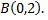
Дата добавления: 2015-08-11; просмотров: 8754;
