Собственные значения и собственные векторы матрицы

Собственные числа и собственные векторы матрицы.

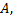Вектор называется собственным вектором матрицы если найдется такое число 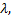что выполняется равенство

т.е. результатом применения к линейного преобразования, задаваемого матрицей 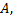является умножение этого вектора на число 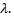Само число 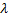называется собственным числом матрицы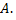

Система уравнений для определения координат собственного вектора

отсюда

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен нулю (правило Крамера). Записав это условие в виде

получим уравнение для определения собственных чисел 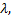называемое характеристическим уравнением. Кратко его можно представить в виде поскольку в его левой части стоит определитель матрицы Многочлен относительно называется характеристическим многочленом матрицы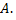

Свойства характеристического многочлена.

1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Так как

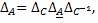но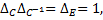

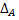следовательно Таким образом, не зависит от выбора базиса. Значит, не изменяется при переходе к новому базису.

2) Если матрица линейного преобразования является симметричной, то все корни характеристического уравнения – действительные числа.