Разложение вектора по базису. Линейные пространства
Если векторы 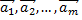 линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Примером линейно независимых векторов является два неколлинеарных вектора
линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Примером линейно независимых векторов является два неколлинеарных вектора 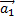 и
и 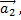 если
если
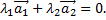
Условие будет выполняться только в том случае, когда 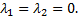 Если
Если 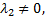 то
то 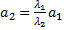 и
и  и
и 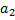 коллинеарны.
коллинеарны.
Свойства векторов линейного пространства.
1) Если среди векторов 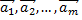 имеется нулевой вектор, то эти векторы линейно зависимы.
имеется нулевой вектор, то эти векторы линейно зависимы.
2) Если часть векторов 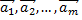 является линейно зависимыми, то все эти векторы линейно зависимые.
является линейно зависимыми, то все эти векторы линейно зависимые.
Рассмотрим пример. Являются ли векторы
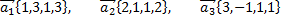
линейно зависимыми?
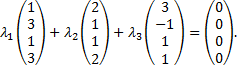
Запишем систему и решим ее
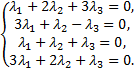
Составим расширенную матрицу по данной системе
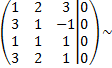
после некоторых элементарных преобразований получим матрицу ступенчатого вида
 .
.
Согласно теореме Кронекера–Капели данная система имеет несколько решений, так как количество строк в основной матрице 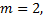 а количество столбцов в основной матрице
а количество столбцов в основной матрице 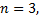 т.е.
т.е. 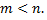 Пусть
Пусть 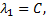 тогда
тогда 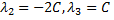 следовательно, векторы линейно зависимые, так как выполняется условие
следовательно, векторы линейно зависимые, так как выполняется условие

не только когда 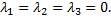
Линейное пространство  называется n-мерным, если в нем существует
называется n-мерным, если в нем существует 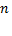 линейно независимых векторов, а любые из
линейно независимых векторов, а любые из 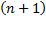 векторов уже являются зависимыми.
векторов уже являются зависимыми.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Совокупность 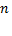 линейно независимых векторов n-мерного пространства
линейно независимых векторов n-мерного пространства  называется базисом.
называется базисом.
Каждый вектор  линейного пространства
линейного пространства  можно представить единственным способом в виде линейной комбинации векторов базиса.
можно представить единственным способом в виде линейной комбинации векторов базиса.
Пусть векторы 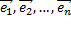 образуют произвольный базис n-мерного пространства
образуют произвольный базис n-мерного пространства 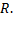 Так как любые из
Так как любые из 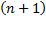 векторов n-мерного пространства
векторов n-мерного пространства  зависимы, то будут зависимы векторы
зависимы, то будут зависимы векторы 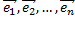 и рассматриваемый вектор
и рассматриваемый вектор  . Тогда существуют такие не равные одновременно нулю числа
. Тогда существуют такие не равные одновременно нулю числа 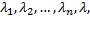 что
что
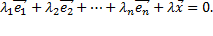
При этом 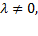 а если
а если 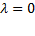 и хотя бы одно из чисел
и хотя бы одно из чисел 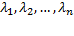 было бы отлично от нуля, то векторы
было бы отлично от нуля, то векторы 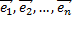 были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,
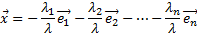
или
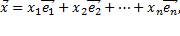
где, 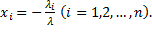 Данное равенство называется разложением вектора
Данное равенство называется разложением вектора  по базису
по базису 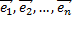 , а числа
, а числа 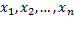 - координатами вектора
- координатами вектора  относительно этого базиса.
относительно этого базиса.
В силу единственности разложения каждый вектор может быть однозначно определен координатами в некотором базисе.
Важно не путать понятие вектора, приведенное выше с понятием вектора как направленного отрезка на плоскости или в пространстве. Направленные отрезки являются всего лишь частным случаем элементов линейного (векторного) пространства. Линейное (векторное) пространство – понятие более широкое. Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д. Если операции сложения и умножения на число определены для действительных элементов, то линейное пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
Контрольные вопросы
1. Дать определение Евклидова пространства.
2. Какие системы векторов называют линейно – независимыми?
3. Записать алгоритм разложения вектора по базису.
4. Дать определение N-мерного векторного пространства.
Дата добавления: 2015-08-11; просмотров: 1489;
