Корреляцияның таңдама коэффициенті.

Кездейсоқ шамалар арасындағы корреляциялық тәуелділіктің ерекшеліктерін толық сипаттау үшін бұл тәуелділіктің түрін анықтау және ол сызықтық тәуелділік болған жағдайда оның күшін регрессия коэффициентінің шамасы бойынша бағалау жеткіліксіз. 3-суретте екі сызықтық корреляциялық тәуелділіктің 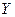-тің Х- ке графиктік суреттемесі келтірілген және регрессияның сәйкес түзу сызықтары бейнеленген.

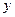
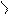
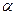
y Одной из важных задач медицинского исследования является изучение связи между фактором, воздействующим на организм, и параметром – откликом на это воздействие, а также моделирование этого параметра в зависимости от действующего фактора. Эта задача решается методами корреляционного и регрессионного анализа.

а) x б) x

3-сурет

Мұндағы 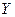және Х шамаларының арасында корреляциялық тәуелділіктің күші бірдей (ол регрессия сызықтарының сәйкес түзулерінің ОХ осіне енкею бұрыштарының теңдігінен шығады). Алайда 3 а) сур. кескінделген корреляциялық тәуелділік үшін бақылау нүктелерінің регрессия сызығына қарасты шашылуы,3 б) сур. кескінделген корреляциялық тәуелділікке қарағанда аз. Мұндай жағдайда, қарастырылып отырған корреляциялық тәуелділіктер тығыздығыменерекшеленеді деп айтады, және 3 а) сур. кескінделген корреляциялық тәуелділік 3 б) сур. келтірілген корреляциялық тәуелділікке қарағанда тығызырақ деп саналады.

Мысалы, орта мектеп оқушыларының жас мөлшері ( 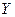) мен олардың мектепте оқып жатқан оқу жылының (Х) арасындағы корреляциялық тәуелділік, сол сияқты жоғары оқу орнындағы студенттерінің жас мөлшерінің оқу жылына тәуелділігіне қарағанда тығыздау болатыны айқын, себебі жоғары оқу орнында бір жылда оқып жатқан студенттердің арасында жас мөлшерлерінде бір сыныпта оқитын оқушыларға қарағанда үлкен алшақтық (шашылу) болатыны байқалады.

Таңдама бақылау нәтижелері бойынша Х және 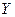шамаларының арасындағы сызықтық корреляциялық тәуелділіктердің тығыздығын бағалау үшін сызықтық корреляцияның таңдама коэффициентіұғымы енгізіледі, және ол

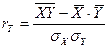(4)

формуласымен анықталады, мұндағы 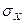және 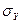- Х және 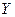шамаларының сәйкес таңдама орта квадраттық ауытқулары және олар

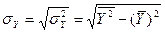(5)

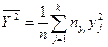
формулаларымен есептелінеді. Айта кету керек, сызықтық корреляцияның таңдама коэффициенті 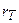-ң негізгі мағынасы, ол сәйкес сызықтық корреляцияның бас коэффициентінің 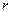эмпирикалық бағасын береді:

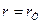(6)

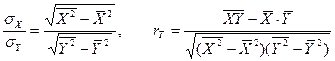
формулаларын ескерсек, 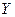- тің Х- ке сызықтық регрессиясының таңдама теңдеуі мына түрде болады:

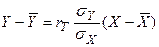(7)

мұндағы 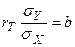(регрессия коэффициенті)

Сол сияқты Х - тің 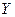-ке сызықтық регрессияның теңдеуін жазуға болады:

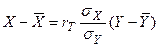(8)

<567 8 9 10 11 >

Дата добавления: 2015-07-22; просмотров: 2274;