Корреляционное отношение
Для оценки тесноты линейной корреляционной связи между признаками в выборке служит выборочный коэффициент корреляции. Для оценки тесноты нелинейной корреляционной зависимости вводят новые свободные характеристики:
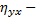 выборочное корреляционное отношение
выборочное корреляционное отношение 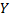 к
к 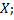
 выборочное корреляционное отношение
выборочное корреляционное отношение  к
к 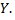
Выборочным корреляционным отношением 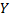 к
к 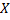 называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака
называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака 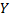
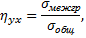
где
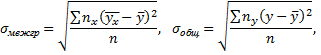
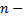 объем выборки,
объем выборки,  частота значения
частота значения  признака
признака  частота значения
частота значения  признака
признака  общая средняя признака
общая средняя признака 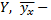 условная средняя признака
условная средняя признака 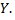
Аналогично определяется выборочное корреляционное отношение  к
к 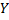
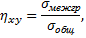
где
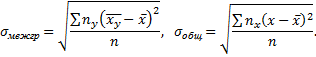
Выборочные корреляционные отношения 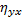 и
и 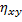 обладают одними и теми же свойствами.
обладают одними и теми же свойствами.
1) Корреляционное отношение удовлетворяет двойному неравенству
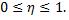
Неравенство 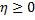 следует из того, что
следует из того, что 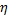 есть отношение неотрицательных чисел – средних квадратических отклонений. Так как
есть отношение неотрицательных чисел – средних квадратических отклонений. Так как

то
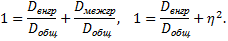
Оба слагаемых неотрицательны и сумма их равна единице, следовательно каждое из них не превышает единицы, т.е. 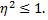 Учитывая, что
Учитывая, что 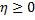 можно заключить, что
можно заключить, что
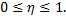
2) Если  то признак
то признак 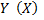 с признаком
с признаком 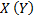 корреляционной зависимостью не связан.
корреляционной зависимостью не связан.
Межгрупповая дисперсия есть дисперсия групповых средних 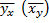 относительно общей средней
относительно общей средней 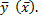 Равенство нулю межгрупповой дисперсии означает, что при всех значениях
Равенство нулю межгрупповой дисперсии означает, что при всех значениях  условные средние сохраняют постоянное значение, равное общей средней. Иными словами, при
условные средние сохраняют постоянное значение, равное общей средней. Иными словами, при 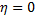 групповая средняя не является функцией от
групповая средняя не является функцией от 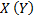 , а значит, признак
, а значит, признак 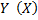 не связан корреляционной зависимостью с признаком
не связан корреляционной зависимостью с признаком 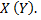
3) Если  то признак
то признак 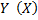 связан с признаком
связан с признаком 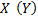 функциональной зависимостью.
функциональной зависимостью.
4) Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции
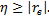
5) Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место точная линейная корреляционная зависимость.
Если график регрессии 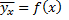 или
или 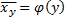 изображаются кривой линией, то корреляцию называют криволинейной.
изображаются кривой линией, то корреляцию называют криволинейной.
Например, функции регрессии 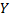 на
на  могут иметь вид параболической корреляции второго порядка
могут иметь вид параболической корреляции второго порядка
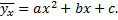
Или, например, могут иметь вид параболической корреляции третьего порядка
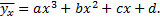
Для определения вида регрессии, строят точки 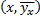 и по их расположению делают заключение о примерном виде функции регрессии. При окончательном решении принимают во внимание особенности, вытекающие из сущности решаемой задачи.
и по их расположению делают заключение о примерном виде функции регрессии. При окончательном решении принимают во внимание особенности, вытекающие из сущности решаемой задачи.
Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции – установление формы и тесноты корреляционной связи. Неизвестные параметры уравнения регрессии ищут методом наименьших квадратов. Для оценки тесноты криволинейной корреляции служат выборочные корреляционные отношения.
Рассмотрим параболическую корреляцию второго порядка, делая предположение, что данные  наблюдений (выборки) позволяют считать, что имеет место именно такая корреляция. В этом случае выборочное уравнение регрессии
наблюдений (выборки) позволяют считать, что имеет место именно такая корреляция. В этом случае выборочное уравнение регрессии 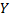 на
на  имеет вид
имеет вид
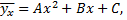
где 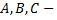 неизвестные параметры.
неизвестные параметры.
Пользуясь методом наименьших квадратов, получают систему линейных уравнений относительно неизвестных параметров
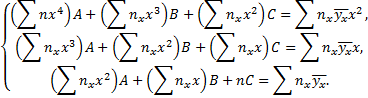
Найденные из этой системы параметры 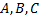 подставляют в уравнение
подставляют в уравнение
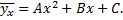
В итоге получают искомое уравнение регрессии.
Рассмотрим пример. Найти выборочное уравнение регрессии 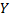 на
на 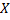 вида
вида
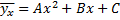
по данным корреляционной таблицы

| 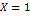
| 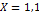
| 
| 
|
| - | ||||
| - | - | |||
| 7,5 | - | |||
| 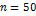
| |||
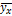
| 6,73 | 7,5 |
Составим расчетную таблицу

| 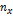
| 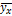
| 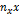
| 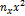
| 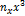
| 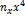
| 
| 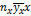
| 
|
| 1,1 | 6,73 | 36,3 | 39,93 | 43,93 | 48,32 | 222,09 | 244,30 | 268,73 | |
| 1,2 | 7,5 | 10,8 | 12,96 | 15,55 | 18,66 | 67,50 | 97,20 | ||
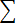
| - | 55,1 | 60,89 | 67,48 | 74,98 | 337,59 | 373,30 | 413,93 |
Используя данные таблицы, составим систему

Решив систему, найдем параметры 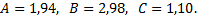 Запишем искомое уравнение регрессии
Запишем искомое уравнение регрессии
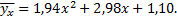
Условные средние, вычисленные по этому уравнению, незначительно отличаются от условных средних корреляционной таблицы. Например, при  найдем по таблице
найдем по таблице 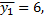 по уравнению
по уравнению  Найденное уравнение хорошо согласуется с данными выборки (наблюдений).
Найденное уравнение хорошо согласуется с данными выборки (наблюдений).
Мы анализировали зависимости между количественными переменными, позволяющими выявить, насколько проявление признака у одного объекта больше, чем у другого.
Дата добавления: 2015-08-11; просмотров: 2549;
