Критерий Колмогорова

На практике кроме критерия 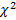часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения 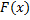и соответствующей теоретической функцией распределения

,

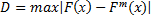которое называют статистикой критерия Колмогорова.

Какова бы ни была функция распределения 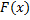непрерывной случайной величины Х, при неограниченном увеличении числа наблюдений

(

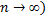
вероятность неравенства стремится к пределу

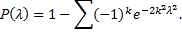
Схема применения критерия Колмогорова следующая:

1)построить эмпирическую функцию распределения 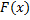и предполагаемую теоретическую функцию распределения ;

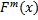2) определить меру расхождения между теоретическим и эмпирическим распределением по формуле

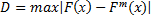
и вычислить величину .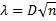

Рекомендуется построить вспомогательную таблицу

	….	….	….	…..

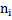
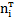
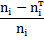
По эмпирическим данным рассчитывается распределение

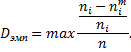
По заданному объему выборки n и уровню значимости определяют табличное значение 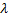и находят

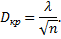
Если вычисленное значение окажется больше критического, то нулевая гипотеза 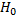о том, что случайная величина 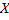имеет заданный закон распределения, отвергается. В противном случае считают, что гипотеза 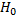не противоречит опытным данным.