Статистическая гипотеза

В процессе работы по статистической обработке данных необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид К, то выдвигают гипотезу: генеральная совокупность распределена по закону К.

Если закон распределения известен, то наверняка неизвестны его параметры. Если есть основания предположить, что неизвестный параметр 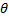равен определенному значению 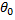, то выдвигают гипотезу, что .

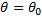Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Примеры статистических гипотез:

1) генеральная совокупность распределена по закону Пуассона;

2) дисперсии двух нормальных совокупностей равны между собой.

Наряду с выдвинутой гипотезой рассматривают противоречащую ей гипотезу.

Основной (нулевой) называют гипотезу .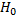

Альтернативной (конкурирующей) называют гипотезу 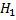, которая противоречит нулевой гипотезе.

Выдвинутая гипотеза может быть как верной, так и неверной. Проверку гипотезы производят статистическими методами. При этом могут быть допущены ошибки первого и второго рода. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода обозначают , ее называют уровнем значимости. Обычно или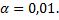

Для проверки нулевой гипотезы используют специально подобранную случайную величину, приближенное распределение которой известно. Обозначают эту случайную величину через Z, если она распределена нормально, через F, если распределена по закону Фишера, через Т, если распределена по закону Стьюдента, через 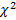, если распределена по закону «хи-квадрат».