Надежность статистических оценок параметров распределения.
Надежностью (доверительной вероятностью) оценки 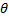 (неизвестный параметр) по
(неизвестный параметр) по  (найденная характеристика по данным выборки) называют вероятность
(найденная характеристика по данным выборки) называют вероятность 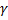 , с которой оценивается неравенство
, с которой оценивается неравенство 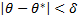
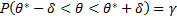 .
.
Надежность оценки задается изначально  ;
;  Доверительным называют интервал
Доверительным называют интервал
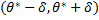 ,
,
который покрывает неизвестный параметр с заданной надежностью.
Рассмотрим выборочную среднюю  как случайную величину
как случайную величину 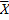 (т.к.
(т.к.  изменяется от выборки к выборке) и выборочные значения признака
изменяется от выборки к выборке) и выборочные значения признака 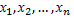 – как одинаково распределенные случайные величины
– как одинаково распределенные случайные величины  . Математическое ожидание каждой из этих величин равно а, а среднее квадратическое отклонение –
. Математическое ожидание каждой из этих величин равно а, а среднее квадратическое отклонение – 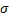 . Параметры распределения
. Параметры распределения 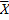
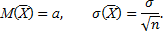
Необходимо, чтобы выполнялось соотношение
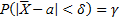 ,
,
где 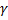 – заданная надежность, которая равна
– заданная надежность, которая равна
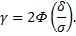
Если учесть, что
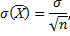
то
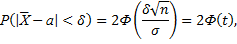
т.е.
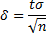
и тогда можно записать
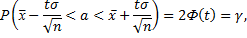
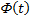 – табличное значение.
– табличное значение.
Таким образом, с надежностью 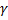 можно утверждать, что рассматриваемый доверительный интервал покрывает неизвестный параметр а и при этом точность оценки равна
можно утверждать, что рассматриваемый доверительный интервал покрывает неизвестный параметр а и при этом точность оценки равна
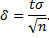
Такую интервальную оценку для неизвестного математического ожидания называют классической. При увеличении надежности классической оценки уменьшается ее точность, а при возрастании объема выборки n число  убывает, и точность оценки увеличивается. Если требуется оценить математическое ожидание с заданной точностью
убывает, и точность оценки увеличивается. Если требуется оценить математическое ожидание с заданной точностью  и надежностью
и надежностью 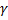 , то минимальный объем выборки, который обеспечит эту точность, находят по формуле
, то минимальный объем выборки, который обеспечит эту точность, находят по формуле
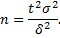
В том случае, если требуется оценить неизвестное математическое ожидание а и при этом неизвестно среднее квадратическое отклонение 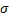 , то пользуются распределением Стьюдента, которое определяется параметром n – объемом выборки и не зависит от неизвестных параметров а и
, то пользуются распределением Стьюдента, которое определяется параметром n – объемом выборки и не зависит от неизвестных параметров а и 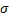
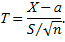
Таким образом, доверительный интервал для математического ожидания будет следующим
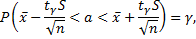
где 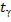 – табличное значение.
– табличное значение.
Случайные величины 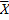 и
и 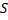 заменены неслучайными величинами
заменены неслучайными величинами  и S, найденными по выборке.
и S, найденными по выборке.
Важно заметить, что для малых выборок объема 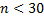 характерно сужение доверительного интервала. Данный факт объясняется тем, что выборка содержит малую информацию об интересующем признаке.
характерно сужение доверительного интервала. Данный факт объясняется тем, что выборка содержит малую информацию об интересующем признаке.
Оценить неизвестное среднее квадратическое отклонение 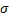 возможно по «исправленному» выборочному среднеквадратическому отклонению
возможно по «исправленному» выборочному среднеквадратическому отклонению 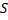 . Необходимо, чтобы выполнялось соотношение
. Необходимо, чтобы выполнялось соотношение
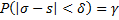 .
.
Если учесть, что
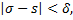
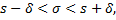
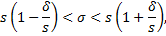
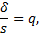
то получим доверительный интервал
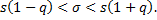
Контрольные вопросы
1. Какими должны быть статистические оценки, чтобы давать хорошие приближения оцениваемых параметров?
2. Что называют надежностью оценки неизвестного параметра?
3. Чему равна сумма произведений отклонений от общей средней на соответствующие им частоты? (ответ пояснить).
4. Что принято использовать для оценки дисперсии генеральной совокупности?
5. Что является характеристикой однородности совокупности?
6. Что служит характеристикой рассеяния вариационного ряда?
Дата добавления: 2015-08-11; просмотров: 1407;
