Определение статистических оценок параметров распределения

Построив вариационный ряд и изобразив его графически, можно получить первоначальное представление о закономерностях, имеющих место в ряду наблюдений, но на практике этого недостаточно. Например, когда необходимо уточнить какие-то сведения о ряде распределения или когда нужно сравнить два ряда.

Пример. Требуется сравнить распределения длин втулок, изготовленных на двух однотипных станках – автоматах. Графики таких распределений имеют почти одинаковый вид, но распределения могут существенно отличаться друг от друга средними значениями случайной величины или рассеиванием данных наблюдений вокруг средних значений.

Для изучения изменения значений случайной величины используют числовые характеристики вариационных рядов (статистические характеристики или оценки), т.е. некоторые постоянные, которые представляют вариационный ряд и отражают присущие изучаемой совокупности закономерности.

К таким постоянным относят:

1) средние величины, вокруг которых концентрируются остальные результаты наблюдений ;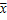

2) показатели вариации или характеристики изменчивости случайной величины – размах варьирования R, среднее квадратическое отклонение 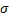, дисперсия 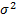и так далее.

Предположим, что требуется изучить количественный признак генеральной совокупности. Если теоретически установлено, что распределение имеет признак, то задача состоит в оценке параметров, которыми определяется это распределение.

Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (найти приближенно) математическое ожидание и среднее квадратическое отклонение, так как эти параметры определяют нормальное распределение. Если признак имеет распределение Пуассона, то стоит оценить параметр 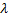, которым это распределение определяется.

Исследователь в своей работе имеет данные выборки (значения количественного признака) 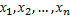, полученные в результате n наблюдений. Через эти данные выражают оцениваемый параметр. Найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны быть:

1) эффективными (эффективнойназывают статистическую оценку, которая при заданном объеме выборки n имеет наименьшую возможную дисперсию);

2) состоятельными (состоятельнойназывают статистическую оценку, которая при 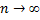стремится по вероятности к оцениваемому параметру). Требование состоятельности предъявляют к статистическим оценкам, если рассматривают выборки большого объема.