Критерий согласия Пирсона

Проверка гипотезы о нормальном распределении генеральной совокупности при заданном уровне значимости .

Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Возможно, что расхождение частот случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий согласия Пирсона отвечает на поставленный выше вопрос, но не доказывает справедливость гипотезы, на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Следует помнить, что объем выборки должен быть достаточно велик (не менее 50).

В качестве критерия проверки нулевой гипотезы принимают случайную величину 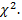Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Чтобы вычислить по эмпирическим данным случайную величину 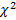, необходимо:

1) вычислить теоретические частоты

где n – объем выборки, h – шаг (разность между соседними вариантами),

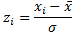
- теоретически рассчитанное значение варианты,

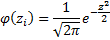
– функция Лапласа, значения которой находят по таблице (прил. 2);

2) составить вспомогательную расчетную таблицу

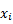
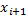
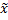
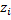
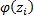
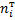
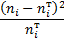
где 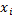– начало интервала (эмпирическая варианта), 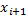– конец интервала (эмпирическая варианта), 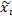– середина интервала, 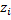– теоретическая варианта, 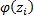– интегральная функция Лапласа, 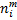– теоретическая частота.

По данным таблицы находят наблюдаемое значение критерия Пирсона

Замечание: интервалы, содержащие малочисленные эмпирические частоты ( 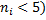следует объединить, а частоты этих интервалов сложить;

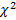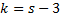3) по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы находят критическую точку 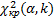, где s – число интервалов, оставшихся после объединения.

Если – нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Если 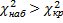– гипотезу отвергают.

Проверка гипотезы о показательном законе распределения случайной величины.

Для этого необходимо:

1) найти выборочное среднее

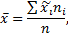
где

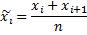
- середина интервала;

2) в качестве оценки параметра 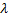показательного распределения принять величину

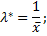
3) найти вероятность попадания Х в частичные интервалы 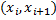по формуле

4) вычислить теоретические частоты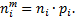

Составить вспомогательную таблицу

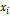
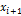
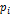
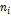
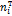
По данным таблицы находят наблюдаемое значение критерия Пирсона

По таблице критических точек распределения находят 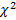(прил. 6), по заданному уровню значимости и числу степеней свободы 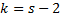, где s – число интервалов после объединения интервалов с малочисленными частотами .

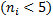Если – нет оснований отвергнуть гипотезу о показательном распределении генеральной совокупности. Если 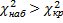– гипотезу отвергают.

Проверка гипотезы о распределении генеральной совокупности по равномерному закону.

Для этого необходимо:

1) оценить концы интервала, в котором распределены возможные значения Х по формулам

,

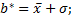
2) найти плотность вероятности предполагаемого распределения

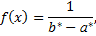
3) найти теоретические частоты

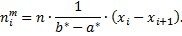
Следует составить вспомогательную таблицу

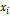
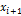
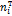
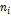
4) сравнить эмпирические и теоретические частоты по критерию Пирсона

приняв число степеней свободы 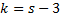, где s – число интервалов, по заданному уровню значимости .

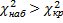Если – нет оснований отвергнуть гипотезу о равномерном распределении генеральной совокупности. Если – гипотезу отвергают.