Однородные диф.ур-я первого порядка

Ф-я f(x,y) наз. однороднойn-ого измерения относительно x и y, если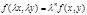

1.

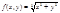
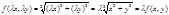
2.

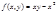
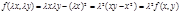
3.

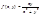
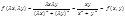однородная функция 0 измерения

Диф.ур-е 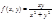наз.однородным ур-ем первого порядка, если ф-я f(x,y) явл. однородной ф-ей нулевого измерения, т.е. .

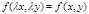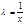
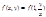
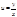
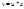
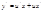
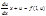
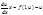
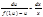
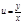
Пример: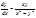

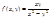
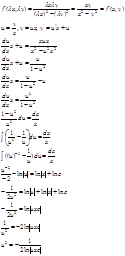
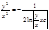
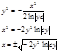
Пример: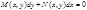

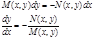функция нулевого измерения

7. Линейные диф.ур-я первого порядка

Уравнение вида y'+ρ(x)y=q(x), где ρ(x) и q(x) заданные функции от x, непрерывные в той области, в которой требуется проинтегрировать уравнение, называется линейным диф.ур-ем первого порядка.

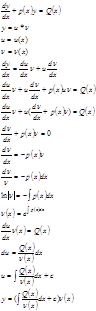
Пример:

Метод вариации произвольной постоянной

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение уравнения (1) ищется в виде

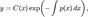где с(х) - новая неизвестная функция от х.

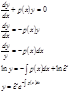
Полагаем, что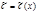

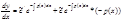
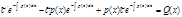
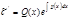
Пример:

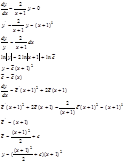
17. Скалярное произведение векторов

Скалярным произведением ненулевого вектора а на ненулевой вектор b наз. число (скаляр) равное произведению длин этих векторов на cos угла между ними (ab, a*b, (ab)).

Т.о. аb=|a|*|b|*cos(a^b). (1)

Замечание: если хотябы один из векторов a или b нулевой, то по определению ab=0.

Свойства скалярного произведения:

6. ab=ba (для любых векторов a и b)

7. (αa)b=α(ab) - для любого числа α

8. (a+b)c=ac+bc

9. если a≠0, то a²>0

Замечание: определение скалярного произведения нами было записано для векторов, кот.явл.направленными отрезками. Для векторов произвольных линейных пространств скалярное произведение определяется по-другому, а именно как отображение, сопоставляющее 2-м векторам число и обладающим св-ми 1-4.

Пусть в пространстве зафиксирован ортонормированный базис {i,j,k} и векторы a(a₁,a₂,a₃) и b(b₁,b₂,b₃). Вычислим скалярное произведение ab.

Заметим, что скалярное произведение ij=|i|*|j|*cos π/2=0

ik=|i|*|k|*cos π/2=0

jk=|j|*|k|*cos π/2=0

i²=j²=k²=1

Имеем ab=(a₁i+a₂j+a₃k)*(b₁i+b₂j+b₃k)=a₁b₁+a₂b₂+a₃b₃

ab= a₁b₁+a₂b₂+a₃b₃ (2)

Рассмотрим частный случай: если b=a

a²= a₁²+ a₂²+ a₃² с другой стороны a²=|a|²

|a|=(3) (длина вектора а)

Из формулы (1) следует, что cos(a^b)=, отсюда из формул (2, 3) получим:

cos(a^b)= (4)