Решение. 1. Определение общей площади составного сечения
1. Определение общей площади составного сечения. Общая площадь составного сечения определяется по формуле:
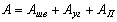 , А = (25,2 + 12,3 + 18)×10-4 = 55,5×10-4 м2.
, А = (25,2 + 12,3 + 18)×10-4 = 55,5×10-4 м2.
2. Определить центр тяжести составного сечения. В качестве вспомогательных осей для определения положения центра тяжести примем горизонтальную и вертикальную оси xшв и yшв , проходящие через центр тяжести швеллера. Статические моменты площади всего сечения относительно этих осей будут равны:
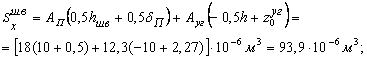

Координаты центра тяжести вычисляем по формулам:
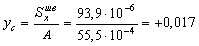 м,
м, 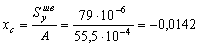 м.
м.
3. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих через его центр тяжести. Для определения указанных моментов инерции составного сечения воспользуемся формулами, выражающими зависимость между моментами инерции относительно параллельных осей:
 (1)
(1)
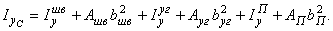 (2)
(2)
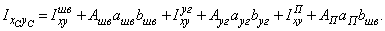 (3)
(3)
В этих формулах расстояние между осями, проходящими через центр тяжести составного сечения, и осями, проходящими через центры тяжести каждой составной части фигуры, а и b (см. рис.), в рассматриваемом случае будут равны:
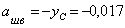 м,
м, 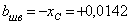 м;
м;
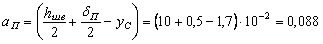 м;
м;
 м.
м.
Подставив числовые значения величин в формулы (1) и (2), получим:
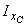 = [1670 + 25,2×(-1,7)2 + 73,4 + 12,3×(-9,43)2 + 1,5 + 18×(8,8)2]×10-8 = 4305,4×10-8 м4.
= [1670 + 25,2×(-1,7)2 + 73,4 + 12,3×(-9,43)2 + 1,5 + 18×(8,8)2]×10-8 = 4305,4×10-8 м4.
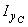 = [139 + 25,2×(1,42)2 + 73,4 + 12,3×(-3,13)2 + 486 +18×(0,14)2]×10-8 = 870,1×10-8 м4.
= [139 + 25,2×(1,42)2 + 73,4 + 12,3×(-3,13)2 + 486 +18×(0,14)2]×10-8 = 870,1×10-8 м4.
При вычислении центробежного момента инерции составного сечения следует иметь в виду, что 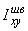 и
и 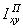 равны 0, так как швеллер и полоса имеют оси симметрии, а
равны 0, так как швеллер и полоса имеют оси симметрии, а
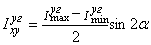 ,
,
где 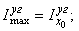

 - угол между осью x и главной осью
- угол между осью x и главной осью 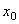 уголка. Этот угол может быть положительным или отрицательным. В нашем примере
уголка. Этот угол может быть положительным или отрицательным. В нашем примере  = +45°, поэтому:
= +45°, поэтому:
 м4.
м4.
Далее, подставив числовые значения в формулу (3), получим величину центробежного момента инерции составного сечения:
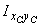 = [0 + 25,2 × (-1,7) × 1,42 + 42,85 + 12,3 × (-9,43) (-3,13) + 0 + 18 × 8,8 × 0,14] ×10-8 = 367,2×10-8 м4.
= [0 + 25,2 × (-1,7) × 1,42 + 42,85 + 12,3 × (-9,43) (-3,13) + 0 + 18 × 8,8 × 0,14] ×10-8 = 367,2×10-8 м4.
4. Найти положение главных центральных осей инерции. Угол наклона главных осей инерции, проходящих через центр тяжести составного сечения, к центральным осям инерции 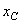 и
и 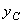 определим по формуле:
определим по формуле:
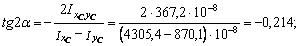
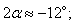
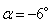 .
.
Так как угол  получился отрицательным, то для отыскания положения главной оси максимального момента инерции u следует ось
получился отрицательным, то для отыскания положения главной оси максимального момента инерции u следует ось 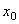 , осевой момент инерции относительно которой имеет наибольшее значение, повернуть на угол
, осевой момент инерции относительно которой имеет наибольшее значение, повернуть на угол  по ходу часовой стрелки. Вторая ось минимального момента инерции v будет перпендикулярна оси u.
по ходу часовой стрелки. Вторая ось минимального момента инерции v будет перпендикулярна оси u.
5. Определить величины главных центральных моментов инерции сечения и проверить правильность их вычисления. Величины главных центральных моментов инерции составного сечения вычисляем по формуле:
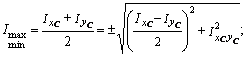
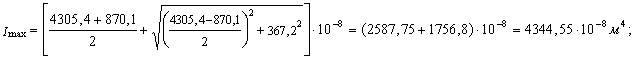

Для контроля правильности вычисления величины моментов инерции составного сечения производим проверки.
1-ая проверка: 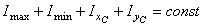 ;
;
Imax + Imin = (4344,55 + 830,95)×10-8 = (5175,5)×10-8 м4;
 = (4305,4 + 870,1)×10-8 = (5175,5)×10-8 м4.
= (4305,4 + 870,1)×10-8 = (5175,5)×10-8 м4.
2-ая проверка: 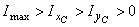 ;
;
4344,55 ×10-8 > 4305,4×10-8 > 870,1×10-8 > 830,95×10-8 м4.
Проверки удовлетворяются, что говорит о правильности вычисления моментов инерции составного сечения.
6. Вычислить величины главных радиусов инерции. Величины главных радиусов инерции вычисляем по известным формулам:
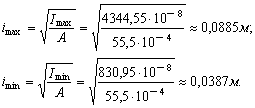
Дата добавления: 2015-08-08; просмотров: 1271;
