Решение. Из сортамента выбираем необходимые данные.
Из сортамента выбираем необходимые данные.
Для уголка равнобокого 90х7 по ГОСТ 8509-89 b = 90 мм, d = 7 мм, z0 = 2,47 см, F1=12,28 см2, Ix1 = Iy1 = 94,3 см4, Imax = 149,67 см4, Imin = 38,94 см4.
Для двутавра по ГОСТ 8239-89 h = 220 мм, b = 110 мм,d =5,7 мм, F2 = 30,6 см2, Ix2 = 2550 см4, IY2 = 157 см4.
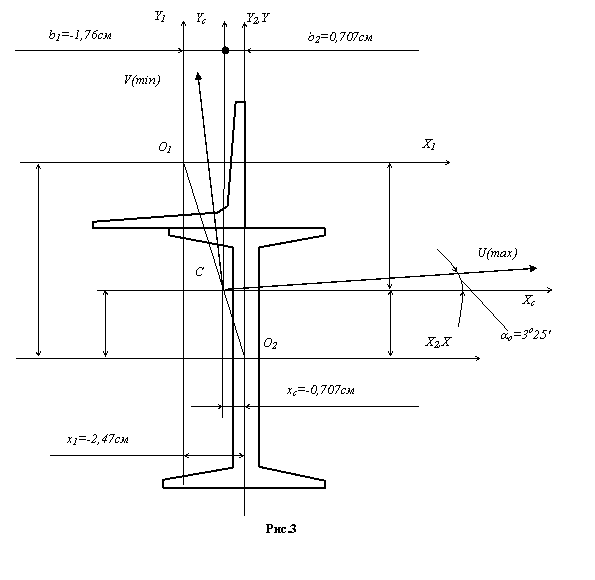
1. Проводим вспомогательную систему осей координат (Х, Y). Начало координат целесообразно расположить в центре тяжести какой-либо из фигур, напримердвутавра (чтобы сократить объём вычислений). Определяем координаты центра тяжести С всей фигуры в системе осей Х и Y:

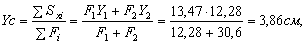
где
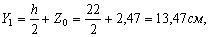
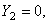

Через центр тяжести С (рисунок 3) проводим центральные оси ХС и YC параллельно проведённым ранее собственным осям уголка и двутавра (Х1, Y1, Х2, Y2).
В системе координат центральных осей ХС и YC координаты центров тяжести уголка и двутавра определяем из выражений
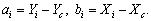
Данные сводим в таблицу 1.
Таблица 1
| Точка | хi, см | yi, см | ai, см | bi, см |
| О1 | - 2,47 | 13,47 | 9,61 | - 1,76 |
| О2 | - 3,86 | 0,707 |
2. Вычисляем осевые и центробежный моменты инерции относительно центральных осей Xс, Yс:
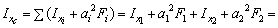
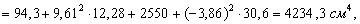
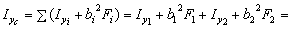
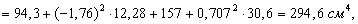
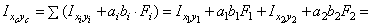
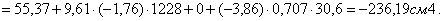
Для равнобокого уголка
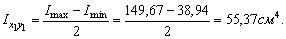
Для двутавра 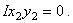
Знак центробежного момента инерции уголка определяем по следующему правилу (см. рис.2):
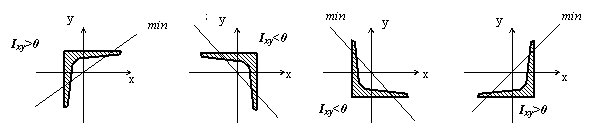
Рис.2
3. Находим угол 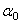 наклона главных центральных осей U и V относительно центральных осей ХС и YC:
наклона главных центральных осей U и V относительно центральных осей ХС и YC:
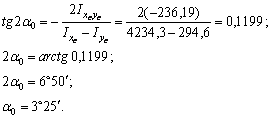
Поскольку угол 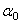 положительный, главная центральная ось U откладывается относительно оси ХС против часовой стрелки, а так как Ixc >Iyc, то ось U является осью, относительно которой момент инерции будет максимальным.
положительный, главная центральная ось U откладывается относительно оси ХС против часовой стрелки, а так как Ixc >Iyc, то ось U является осью, относительно которой момент инерции будет максимальным.
4. Вычисляем главные моменты инерции
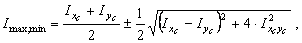
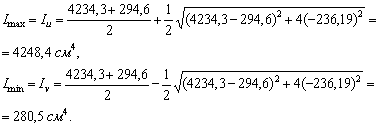
5. Проверка
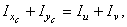
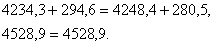
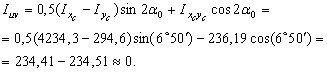


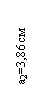
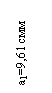
Дата добавления: 2015-08-08; просмотров: 969;
