Задача №22

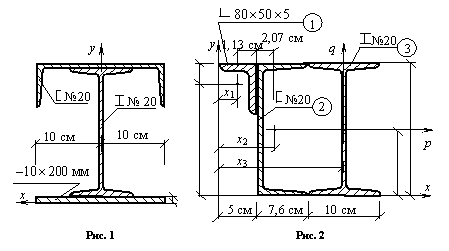
Определить положение центра тяжести составного сечения, показанного на рис. 1.

Вычислить статические моменты S_x, S_y сложного составного сечения (рис.2). Определить площадь этого сечения и найти координаты его центра тяжести.

Решение к рис 2. Предлагается следующий порядок решения.

Если поперечное сечение не содержит осей симметрии, то случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте. Каждому прокатному профилю присваивается порядковый номер.

Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i – го профиля относительно случайных осей х, у; А_i – площадь сечения i – го профиля, А – площадь поперечного сечения всего составного сечения, n – число профилей.

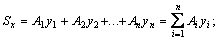
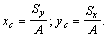Затем вычисляются статические моменты всего сечения по формулам , а по формулам находятся координаты центра тяжести.

Следуя предложенной методике, выпишем (рис. 2): А₁ = 6,36 см²; А₂ = 23,4 см²; А₃ = 26,8 см²; А = 56,56 см²; х₁ = 3,87 см; х₂ = 7,07 см; х₃ = =17,6 см; у₁ = 17,4 см; у₂ = 10 см; у₃ = 10 см.

По формулам 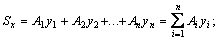находим

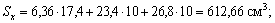
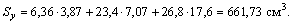
И наконец, с помощью формул 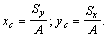определяем координаты центра тяжести всего сечения:

Для проверки полученных результатов рекомендуем самостоятельно определить координаты центра тяжести составного сечения относительно осей p, q (рис. 2).

Ответ к рис.1: x_c = 11,7 см; y_c = 10,83 см.

Ответ к рис.2: x_c = 0; y_c = 10,83 см.