Оценки выборочной совокупности
Под оценкой понимают некоторое значение характеристики соответствующей совокупности, полученное при соответствующих исследованиях.
Все оценки, которые мы с вами рассматриваем, подразделяют на 2 класса:
Классы оценок:
— точечные;
— интервальные.
Точечные параметры — определенное значение параметров, полученное по выборочной совокупности.
Точечная оценка является некоторым одним числом, полученным при соответствующем анализе (например, выборочное (статистическое) среднее (математическое ожидание), выборочная (статистическая) дисперсия – точечные оценки). Но в случае маленького числа попыток эти оценки могут привести к значительным ошибкам. В таком случае используют интервальные параметры. Интервальные оценки определяется двумя числами - границами интервала, в котором находится истинное значение изучаемого параметра, которое оценивается с заданной вероятностью. Таким образом, задача сводится к определению такого интервала (надёжного или доверительного интервала), который с заданной вероятностью (надёжностью) охватывает оцениваемый параметр.
Основные точечные оценки выборочной совокупности:
1. Точечные оценки отличаются тем, что они всегда показывают положение центра эмпирического распределения случайной величины.
а) статистической оценкой для математического ожидания служит среднее арифметическое значение случайной величины (выборочное среднее): 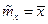
mx — математическое ожидание — эксперимент ещё не произошел
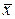 — среднее арифметическое (выборочное среднее) — эксперимент произошел, определяем соответствующие характеристики. Среднее арифметическое - это статистическая характеристика, которая отражает только типичные проявления признака в исследуемой совокупности.
— среднее арифметическое (выборочное среднее) — эксперимент произошел, определяем соответствующие характеристики. Среднее арифметическое - это статистическая характеристика, которая отражает только типичные проявления признака в исследуемой совокупности.
Оценка математического ожидания (выборочное среднее) для несгруппированных данных определяется:
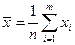
n — объем выборки;
xi — варианты.
Пример исходных данных, представленых в несгруппированном виде:
| Студенты | Таня | Петя | Вася | Лена | Гена | Вера | Лера | Гера | Надя | Ваня |
Оценки 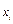
| 4 | 3 | 5 | 3 | 5 | 4 | 3 | 4 | 4 | 2 |
Тогда среднюю успеваемость группы мы можем найти по формуле:
4+3+5+3+5+4+3+4+4+2 / 10 = 3,7
Для сгруппированных данных такая характеристика определяется следующим образом:
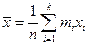 ,
,
k — число интервалов;
mi — частота интервалов.
Пример исходных данных, представленных в сгруппированном виде:
Приведённая выше таблица может быть представлена сгруппированными данными. Тогда значения, которые принимает случайная величина Х (пятибалльная система оценивания) будут записаны в первой строке таблицы, а количество студентов, которые эти оценки получили — во второй.
| Х | 1 | 2 | 3 | 4 | 5 | Итого |
| Кол-во студентов mi | 0 | 1 | 3 | 4 | 2 | 10 студентов |
где mi – количество студентов, обладающих какой-либо оценкой, k=5, n=10 . Тогда (1*0+2*1+3*3+4*4+5*2) /10 = 3,7.
Математическое ожидание имеет вероятностный характер. Это отражается в законе больших чисел. Эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения.
Мода, медиана – также точечные характеристики случайных величин.
2. Характеристики рассеяния
Среднее значение не дает полной информации об изучаемой величине. Например, здесь отсутствуют признаки отклонения изучаемой величины относительно своего среднего значения. Например, могут быть 2 признака, у которых среднее значение абсолютно одинаковое, а рассеяние совершенно разное. Тогда и вводят характеристики рассеяния изучаемых величин.
а) размах вариаций – показатель, определяющий насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака. Зависимость для его расчета имеет вид
R = xmax – xmin
б) Дисперсия показывает степень разбросанности (рассеяния) значений изучаемого признака относительно среднего арифметического.
Дисперсия показывает среднюю сумму квадратов всех отклонений изучаемой величины от их средней величины.
Статистическая оценка для дисперсии для несгруппированных данныхопределяется:
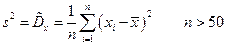 (1)
(1)
Статистическая оценка для дисперсии для сгруппированных данных:
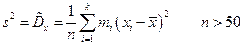 (2)
(2)
Если объем выборки < 50 ед (n < 50), то для получения несмещенной оценки дисперсии деление осуществляется не на n, а на (n – 1), т. е. имеют следующее соотношение:
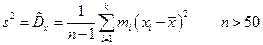
Статистическая оценка для среднеквадратического отклонения 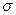 –
– 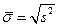 .
.
При практических вычислениях формулы (1)-(2) можно также применять (соответственно) в виде:
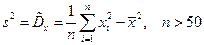 - для несгруппированных данных
- для несгруппированных данных
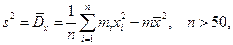 - для сгруппированных данных
- для сгруппированных данных
в) В эконометрических исследованиях применяется и другая важная характеристика рассеяния, это коэффициент вариации. Оценка его:
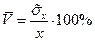 ,
,
где 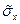 — оценка среднеквадратического отклонения.
— оценка среднеквадратического отклонения.
Коэффициент вариации— показывает относительную меру рассеяния признака. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Для системы случайных признаков определяют корреляционный момент и коэффициент корреляции.
г) Корреляционный момент — изучает зависимость признаков между собой (признаки могут быть независимы между собой или иметь вероятностную зависимость).
С другой стороны, корреляционный момент показывает величину математического ожидания отклонений изучаемых признаков относительно своих средних:
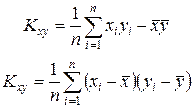
д) Чтобы обезразмерить коэффициент ковариации используют коэффициент корреляции:
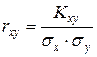
Дата добавления: 2015-08-26; просмотров: 2212;
