Модели функции S

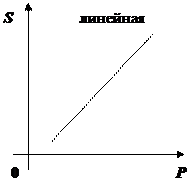
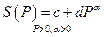, S(Р) = C + dР, где

с, d — параметры связи цены и величины предложения, определяемые на основе конкретных наблюдений и статистических вычислений (в частности, методом наименьших квадратов), d - всегда положительная величина

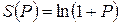
Эластичность предложения S по Р (ценовая эластичность) показывает на какую величину изменится объём предложения S товара при изменении его цены P на 1 единицу и определяется по формуле:

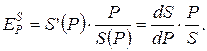
Такая функция будет положительной,т.к. цена и величина предложения изменяются в одном направлении.

В статистических условиях функци S являются однородными функциями нулевого измерения относительно цены Р.

Это положение означает, что предложение труда зависит не от денежной, а от реальной заработной платы.

Однородность функции S понимают следующим образом, если цены и доходы изменятся в одной и то же пропорции, то значение предложения не изменится.

Как и в случаях функции D, так и в случае функции S, экономическая теория не дает отправных точек для нахождения форм таких функций.

Форма таких функций выявляется исключительно путем статистических исследований для определения группы товаров, однако, необходимо отметить, что экономическая теория, как правило, проводит анализ таких функций на одной координатной плоскости, а затем уже делается вывод о состоянии рынка.

Рассмотрим такой подход:

Такой подход в исследовании рынка отличается некоторой упрощенностью, но полученные результаты могут быть экстраполированы на общий многомерный случай.

Соответствующая точка пересечения E — точка равновесия P : P = 100; при P < 100 D(Р) > S(P) — на рынке наблюдается дефицит;

при P > 100 D(P) < S(P) — остаётся нереализованная продукция.

Рассмотрим вариант динамической модели рынка одного продукта (товара). Тогда возможны три варианта поведения рыночной цены P(t) во времени и три варианта характера рыночного равновесия (соответственно):

I.Характер рыночного равновесия устойчивый:

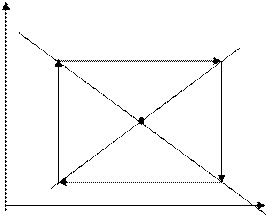
III.Рынок испытывает регулярные колебания постоянной амплитуды:

		P

В связи с тем, что траектории рыночной цены соответствует геометрическая интерпретация, похожая на паутину (см.рис.I-III), данная динамическая модель рынка и получил название «паутинообразной модели».