Связь предельной прибыли и эластичности спроса по цене

Пусть Q – количество товара,

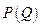– цена на товар, (тогда 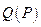- спрос на товар, т.е. ),

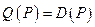R(Q) – суммарная прибыль от реализации товара (выручка), которая определяется произведением проданного количества товара на цену:

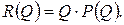
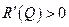Поведение функции R при росте её аргумента Q, как известно, можно определить, исходя из знака её производной (когда , функция 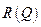возрастает, когда 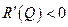– функция 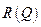убывает). Т.е. для нахождения ответа на вопрос о росте или снижении суммарной прибыли (выручки) достаточно определить знак производной , которую назовём функцией предельной прибыли.

Предельную прибыль находим по соотношению:

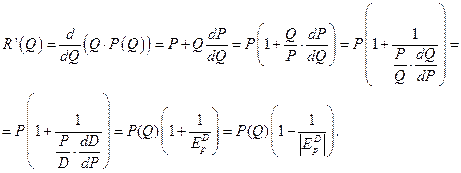
Проанализируем знак полученного выражения (с учётом того, что цена 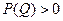). Рассмотрим возможные случаи эластичности спроса:

1. При реализации товара неэластичного спроса 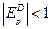дробь 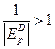, выражение 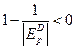, тогда предельное значение прибыли 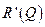отрицательное и тогда суммарная прибыль 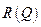падает.

2. При реализации товара эластичного спроса 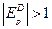дробь 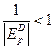, выражение 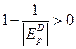, тогда предельное значение прибыли 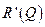положительное и суммарная прибыль 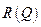увеличивается.

3. При реализации товара единичной эластичности спроса 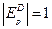дробь 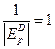, выражение 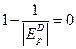, тогда предельное значение прибыли 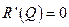и суммарная прибыль 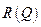не изменяется ни при росте, ни при падении цены.

В этой связи особо ценным будет утверждение: для товаров эластичного спроса суммарная прибыль - функция возрастающая, а для товаров неэластичного спроса - убывающая.

Определение эластичности спроса по цене, если цена представлена функцией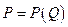

Пусть цена на товар задана функцией 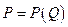. Тогда, как было отмечено ранее 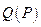- спрос на товар, который является обратной функцией к функции 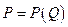, причём, .

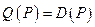Для того, чтобы определить функцию эластичности спроса

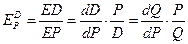
в этом случае, для нахождения 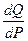предварительно напомним из курса высшей математики как находится производная обратной функции.

Пусть 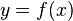- функция от аргумента x. Если в уравнении 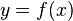y считать аргументом, а x - функцией, то возникает новая функция 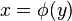, где 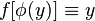- функция обратная данной. Тогда производная обратной функции равна обратной величине производной данной функции, т.е.

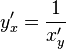
Тогда, с учётом сказанного, производная обратной функции будет иметь вид .

И функцию эластичности спроса перепишем тогда в виде: