Основные законы распределения дискретных случайных величин.
1 Закон распределения Бернулли. Случайная величина Х, распределенная по закону Бернулли, принимает значения 1- успех или 0 - неудача, с вероятностями p и q соответственно (p+q=1).
| xi | ||
| pi | q | p |
2. Биномиальный закон распределения. Случайная величина X принимает значения: 0, 1, 2, 3, 4, 5,…, n , с вероятностью, определяемой по формуле Бернулли (1.24):
| xi | … | к | … | n | |||
| pi |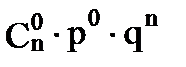 
| 
| 
| … | 
| … | 
|
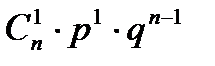
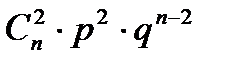
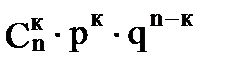
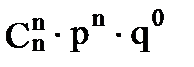
3. Закон распределения Пуассона. Случайная величина Х принимает бесконечное счетное число значений: 0, 1, 2, 3, 4, 5,…, к ,… , с вероятностью, определяющейся по формуле Пуассона:
Р(Х=к)=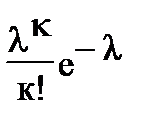 
, (2.2)
где l>0 - параметр распределения Пуассона.
| xi | … | к | … | |||
| pi |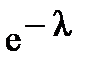 
| 
| 
| … | 
| … |
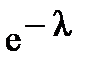
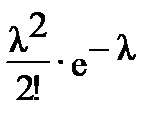
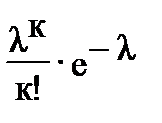
При n 
и p 0 биномиальный закон приближается к закону распределения Пуассона, где l=np.
4. Геометрический закон распределения. Пусть P(А)=p- вероятность наступления события А в каждом опыте, соответственно, q=1-p - вероятность не наступления события А (схема Бернулли).
Вероятность появления к - неудач до первого наступления события А определяется по формуле:
P(X=m)=p×qm. (2.3)
Случайная величина Х распределенная по геометрическому закону принимает значения: 0,1,2,…,к,…, с вероятностью, определяемой по формуле (2.3):
| xi | … | m | … | |||
| рi | p | pq | pq2 | … | Pqm | … |
5. Геометрический закон распределения сдвинутый на единицу.
Вероятность наступления события А в m-ом опыте определяется по формуле:
P(X=к)=p×qm-1. (2.4)
Случайная величина Х - распределенная по геометрическому закону, сдвинутому на 1 (геометрический закон +1), означает число опытов до первого появления события А и принимает значения: 1, 2,…,к,… , с вероятностью, определяемой по формуле (2.4):
| xi | … | к | … | |||
| рi | p | pq | pq2 | … | pqк-1 | … |
6. Отрицательное биномиальное распределение. Если производится ряд независимых опытов в каждом из которых событие А появляется с вероятностью р, до получения m успехов (m=0,1,2,…),то при этом вероятность Х=к "неудачных" опытов можно определить по формуле:
(к = 0,1,2,...). (2.5)
Вероятность появления к-неудач, до получения m-успехов совпадает с m-ым членом разложения выражения qк(1-р)-к по степеням р, т.е. отрицательного бинома (отсюда и название):
.
Распределение определяется двумя параметрами «m» и «р».
2) Равномерное распределение
Случайная величина X распределена по равномерному (прямоугольному) закону, если ее функция плотности вероятностей принимает постоянное значение на промежутке (a.b) и равна нулю вне его.
Дифференциальная функция равномерного закона на интервале (a,b)
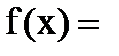
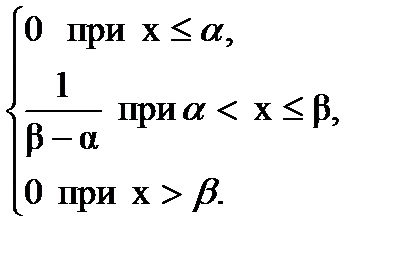(4.1)
Интегральная функция равномерного закона на интервале (a,b) (рис.11):
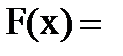
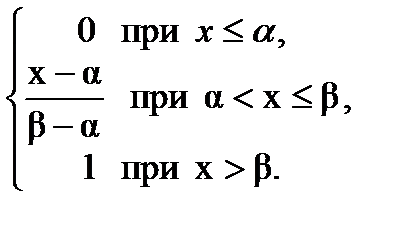(4.2)
Основные числовые характеристики равномерного закона:
1. Математическое ожидание:
= 
= 
== 
= 
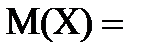
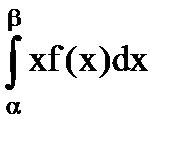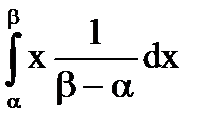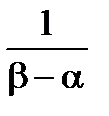
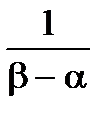
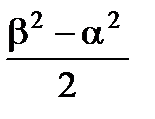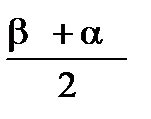. (4.3)
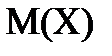совпадает, в силу симметрии распределения, с медианой.
2. Моды равномерное распределение не имеет.
3. Дисперсия: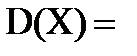 
= 
=
= 
= 
- 
= 
-
- 
= 
= 
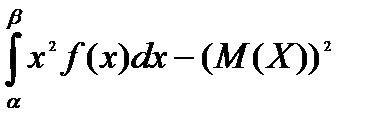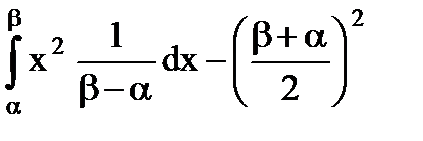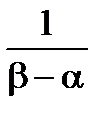
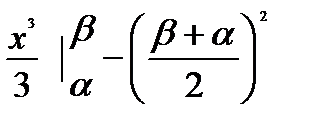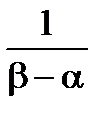
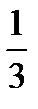
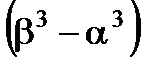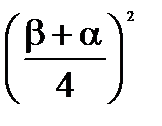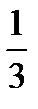
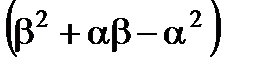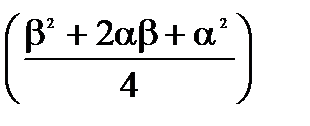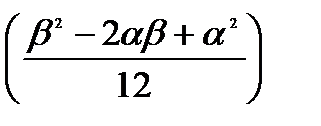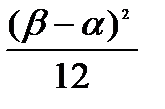. (4.4)
Отсюда, среднее квадратическое отклонение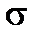 
(x)=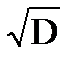 
= 
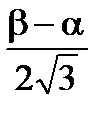. (4.5)
6. Вероятность попадания случайной величины в заданный интервал (a;b).
= 
= 
= 
= 
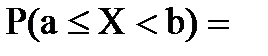
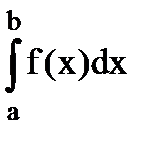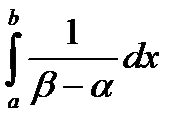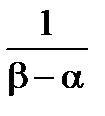
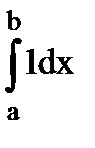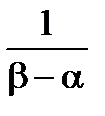
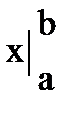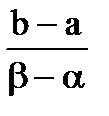. (4.6)
Дата добавления: 2015-08-11; просмотров: 1036;