Дифференциальная функция (плотность распределения) непрерывной случайной величины и ее свойства.

Случайная величина X непрерывна, если ее интегральная функция непрерывна на всей числовой оси. Случайная величина X непрерывна и имеет дифференциальную функцию, если ее интегральная функция непрерывна и дифференцируема всюду, за исключением конечного числа точек на любом конечном промежутке.

Дифференциальной функцией (функцией плотности вероятности) случайной величины X называется производная ее функции распределения:

f(x)= 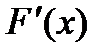. (3.2)

С помощью дифференциальной функции можно получить формулу вероятности попадания случайной величины X в заданный интервал:

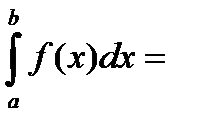
P( )= 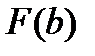- 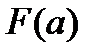. (3.3)

Свойства дифференциальной функции:

1)f(x) 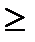0;

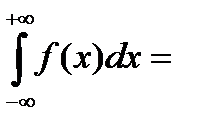2) 1;

3) F(x)= .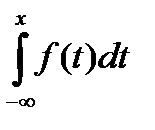

3)Числовые характеристики непрерывных случайных величин

1) Математическое ожидание непрерывной случайной величины X определяется по формуле:

M(X)= 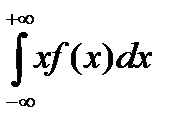. (3.4)

Если непрерывная случайная величина X определена на интервале (а; b), то:

M(X)= 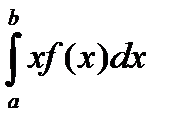. (3.5)

2) Мода непрерывной случайной величины X будет определяться как максимум ее дифференциальной функции:

M_о(X) 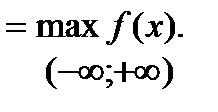(3.6)

3) Медиана определяется как значение случайной величины, которое делит площадь под дифференциальной функцией на две равные части.

M_е(X): 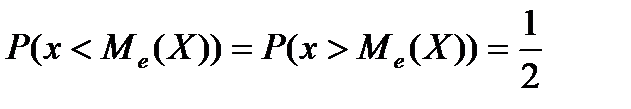. (3.7)

4)Дисперсиянепрерывной случайной величины :

D(X)= 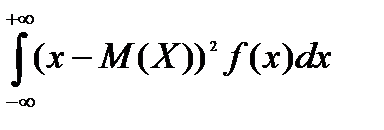= 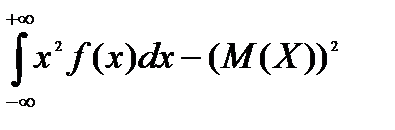. (3.8)

Все свойства дисперсии и математического ожидания, установленные для ДСВ, сохраняются для НСВ.

Если распределение симметрично, то его мода, медиана и математическое ожидание совпадают.